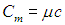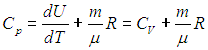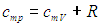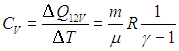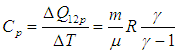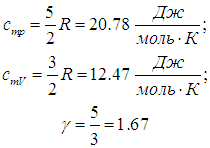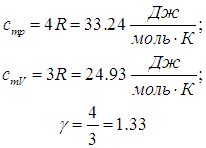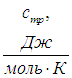2.3. Теплоемкость системы

Введем теперь очень важную термодинамическую характеристику, называемую теплоемкостью системы (традиционно обозначается буквой С с различными индексами).

Теплоемкость — величина аддитивная, она зависит от количества вещества в системе. Поэтому вводят также удельную теплоемкость

и молярную теплоемкость

Поскольку количество теплоты не есть функция состояния и зависит от процесса, теплоемкость также будет зависеть от способа подвода тепла к системе. Чтобы понять это, вспомним первое начало термодинамики. Разделив равенство (2.4) на элементарное приращение абсолютной температуры dT, получим соотношение

Второе слагаемое, как мы убедились, зависит от вида процесса. Отметим, что в общем случае неидеальной системы, взаимодействием частиц которой (молекул, атомов, ионов и т. п.) пренебречь нельзя (см., например, § 2.5 ниже, в котором рассматривается ван–дер–ваальсовский газ), внутренняя энергия зависит не только от температуры, но и от объема системы. Это объясняется тем, что энергия взаимодействия зависит от расстояния между взаимодействующими частицами. При изменении объема системы меняется концентрация частиц, соответственно, меняется среднее расстояние между ними и, как следствие, меняется энергия взаимодействия и вся внутренняя энергия системы. Другими словами, в общем случае неидеальной системы

.

Поэтому, в общем случае первое слагаемое нельзя писать в виде полной производной, полную производную необходимо заменить на частную производную с дополнительным указанием на то, при какой постоянной величине она вычисляется. Например, для изохорного процесса:

.

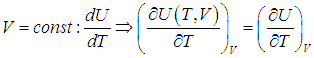Или для изобарного процесса

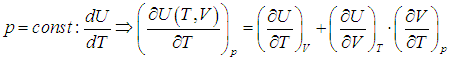
Входящая в это выражение частная производная 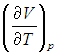 вычисляется с помощью уравнения состояния системы, записанного в виде . Например, в частном случае идеального газа

,

эта производная равна

.

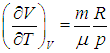Мы рассмотрим два частных случая, соответствующих процессу подведения теплоты:

• постоянном объеме;
• постоянном давлении в системе.

В первом случае работа dА = 0 и мы получаем теплоемкость С_V идеального газа при постоянном объеме:

С учетом сделанной выше оговорки, для неидеальной системы соотношение (2.19) необходимо записать в следующем общем виде

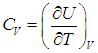
Заменив в 2.7 на , а  на  немедленно получаем:

.

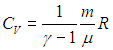Для вычисления теплоемкости идеального газа С_p при постоянном давлении (dp = 0) мы учтем, что из уравнения (2.8) следует выражение для элементарной работы при бесконечно малом изменении температуры

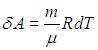
Получаем в итоге

Разделив это уравнение на число молей вещества в системе, получаем аналогичное соотношение для молярных теплоемкостей при постоянном объеме и давлении, называемое соотношением Майера

Приведем для справки общую формулу — для произвольной системы — связывающую изохорную и изобарную теплоемкости:

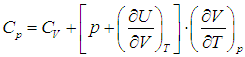
Выражения (2.20) и (2.21) получаются из этой формулы путем подстановки в неё выражения для внутренней энергии идеального газа  и использования его уравнения состояния (см. выше): 

.

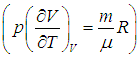Теплоемкость данной массы вещества при постоянном давлении больше теплоемкости при постоянном объеме, так как часть подведенной энергии тратится на совершение работы и для такого же нагревания требуется подвести больше теплоты. Отметим, что из (2.21) следует физический смысл газовой постоянной:

Таким образом, теплоемкость оказывается зависящей не только от рода вещества, но и от условий, в которых происходит процесс изменения температуры.

Как мы видим, изохорная и изобарная теплоемкости идеального газа от температуры газа не зависят, для реальных веществ эти теплоемкости зависят, вообще говоря, также и от самой температуры Т.

Изохорную и изобарную теплоемкости идеального газа можно получить и непосредственно из общего определения, если воспользоваться полученными выше формулами (2.7) и (2.10) для количества теплоты, получаемого идеальным газом при указанных процессах.

Для изохорного процесса выражение для С_V следует из (2.7):

Для изобарного процесса выражение для С_р вытекает из (2.10):

Для молярных теплоемкостей отсюда получаются следующие выражения

Отношение теплоемкостей равно показателю адиабаты:

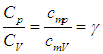
На термодинамическом уровне нельзя предсказать численное значение g; нам удалось это сделать лишь при рассмотрении микроскопических свойств системы (см. выражение (1.19), а также (1.28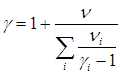) для смеси газов). Из формул (1.19) и (2.24) следуют теоретические предсказания для молярных теплоемкостей газов и показателя адиабаты.

Одноатомные газы (i = 3):

Двухатомные газы (i = 5):

Многоатомные газы (i = 6):

Экспериментальные данные для различных веществ приведены в таблице 1.

Таблица 1

Видно, что простая модель идеальных газов в целом неплохо описывает свойства реальных газов. Обращаем внимание, что совпадение было получено без учета колебательных степеней свободы молекул газа.

Мы привели также значения молярной теплоемкости некоторых металлов при комнатной температуре. Если представить кристаллическую решетку металла как упорядоченный набор твердых шариков, соединенных пружинками с соседними шариками, то каждая частица может только колебаться в трех направлениях (i_кол = 3), и с каждой такой степенью свободы связаны кинетическая k_ВТ/2 и такая же потенциальная энергия. Поэтому на частицу кристалла приходится внутренняя (колебательная) энергия k_ВТ. Умножая на число Авогадро, получим внутреннюю энергию одного моля

откуда вытекает значение молярной теплоемкости

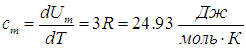
(Вследствие малого коэффициента теплового расширения твердых тел для них не различают с_р и c_v). Приведенное соотношение для молярной теплоемкости твердых тел называется законом Дюлонга и Пти, и из таблицы видно хорошее совпадение расчетного значения

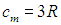
с экспериментом.

Говоря о неплохом соответствии приведенных соотношений и данных опытов, следует отметить, что оно наблюдается лишь в определенном диапазоне температур. Иначе говоря, теплоемкость системы зависит от температуры, и формулы (2.24) имеют ограниченную область применения. Рассмотрим сначала рис. 2.10, на котором изображена экспериментальная зависимость теплоемкости с_тV газообразного водорода от абсолютной температуры Т.

Рис. 2.10. Молярная теплоемкость газообразного водорода Н₂ при постоям ном объеме как функция температуры (экспериментальные данные)

Ниже, для краткости, говорится об отсутствии у молекул тех или иных степеней свободы в определенных температурных интервалах. Еще раз напомним, что речь в действительности идет о следующем. По квантовым причинам, относительный вклад во внутреннюю энергию газа отдельных видов движения действительно зависит от температуры и в определенных температурных интервалах может быть мал настолько, что в эксперименте — всегда выполняемом с конечной точностью — он незаметен. Результат эксперимента выглядит так, как будто этих видов движения нет, нет и соответствующих степеней свободы. Число и характер степеней свободы определяются структурой молекулы и трехмерностью нашего пространства — от температуры они зависеть не могут.

Вклад во внутреннюю энергию от температуры зависит и может быть мал.

 

При температурах ниже 100 К теплоемкость

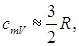
что указывает на отсутствие у молекулы как вращательных, так и колебательных степеней свободы. Далее с ростом температуры теплоемкость быстро возрастает до классического значения

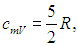
характерного для двухатомной молекулы с жесткой связью, в которой нет колебательных степеней свободы. При температурах свыше 2 000 К теплоемкость обнаруживает новый скачок до значения

Этот результат свидетельствует о появлении еще и колебательных степеней свободы. Но все это пока выглядит необъяснимым. Почему молекула не может вращаться при низких температурах? И почему колебания в молекуле возникают лишь при очень высоких температурах? В предыдущей главе дано краткое качественное рассмотрение квантовых причин подобного поведения. А сейчас можно лишь повторить, что все дело сводится к специфически квантовым явлениям, не объяснимым с позиций классической физики. Эти явления подробно рассмотрены в последующих разделах курса.

 

Дополнительная информация

http://www.plib.ru/library/book/14222.html — Яворский Б.М., Детлаф А.А. Справочник по физике, Наука, 1977 г. — стр. 236 — таблица характеристических температур «включения» колебательных и вращательных степеней свободы молекул для некоторых конкретных газов;

 

Обратимся теперь к рис. 2.11, представляющему зависимость молярных теплоемкостей трех химических элементов (кристаллов) от температуры. При высоких температурах все три кривые стремятся к одному и тому же значению

соответствующему закону Дюлонга и Пти. Свинец (Рb) и железо (Fe) практически имеют это предельное значение теплоемкости уже при комнатной температуре.

Рис. 2.11. Зависимость молярной теплоемкости для трех химических элементов - кристаллов свинца, железа и углерода (алмаза) —  от температуры

Для алмаза же (С) такая температура еще не достаточно высока. А при низких температурах все три кривые демонстрируют значительное отклонение от закона Дюлонга и Пти. Это еще одно проявление квантовых свойств материи. Классическая физика оказывается бессильной объяснить многие наблюдаемые при низких температурах закономерности.

 

Дополнительная информация

http://eqworld.ipmnet.ru/ru/library/physics/thermodynamics.htm — Я. де Бур Введение в молекулярную физику и термодинамику, Изд. ИЛ, 1962 г. — стр. 106–107, ч. I, § 12 — вклад электронов в теплоемкость металлов при температурах близких к абсолютному нулю;

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_82.htm — Перельман Я.И. Знаете ли вы физику? Библиотечка «Квант», выпуск 82, Наука,1992г. Стр. 132, вопрос 137: какие тела обладают наибольшей теплоемкостью (ответ смотри на стр. 151);

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_82.htm — Перельман Я.И. Знаете ли вы физику? Библиотечка «Квант», выпуск 82, Наука,1992г. Стр. 132, вопрос 135: о нагревании воды в трех состояниях — твердом, жидком и парообразном (ответ смотри на стр. 151);

http://www.femto.com.ua/articles/part_1/1478.html — физическая энциклопедия. Калориметрия. Описаны методы измерения теплоемкостей.