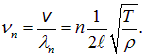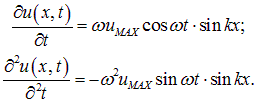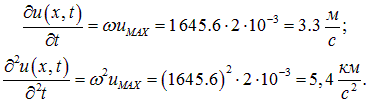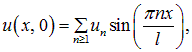Гармоники

На струне, закрепленной на одном конце, могут существовать колебания любых частот. Закрепим теперь второй конец струны в точке с координатой . Имеем то же решение (2.53), которое должно удовлетворять дополнительному граничному условию:

Это означает, что

На струне длиной l, закрепленной на обоих концах, могут существовать только стоячие волны с волновыми векторами

Соответственно, длины волн будут

Иными словами, на длине струны должно укладываться целое число полуволн. Следовательно, закрепленная с обоих концов струна может колебаться только с определенными частотами:

Мы использовали здесь уравнение (2.2) для скорости волн на натянутой струне.

Из (2.58) видно, что частота колебаний повышается при:

• уменьшении длины струны;
• уменьшении ее толщины (линейной плотности);
• увеличении натяжения.

Эти закономерности известны каждому, кто держал в руках хотя бы гитару. Колебания с низшей частотой (n = 1) называются основной (первой) гармоникой, с последующими частотами — высшими (второй, третьей и т. п.) гармониками.

Аналогичные граничные условия существуют и для колебаний воздуха в трубах духовых музыкальных инструментов. Соответственно, в их сигналах также присутствуют только вполне определенные частоты. Рассмотрим, например, органную трубу длиной l. Волна давления в ней также может быть описана уравнением вида (2.53):

Если труба открыта с обеих сторон, то давление на концах равно стационарному (атмосферному) и  в точках х = 0, l. Отсюда получаем те же условия для волновых чисел

длин волн

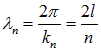
и частот

Если же труба открыта в точке х = 0 и закрыта на другом конце (х = l), то на закрытом конце смещение частиц равно нулю, а давление достигает максимума или минимума:

Отсюда следуют несколько иные соотношения:

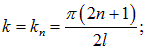
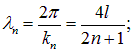
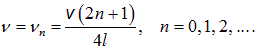
Первая гармоника для такой трубы возбуждается на частоте

что в два раза меньше частоты

первой гармоники полностью открытой трубы.

Пример 3. Нейлоновая гитарная струна имеет линейную плотность массы 7.2 г/м и натянута с силой 150 Н. Длина струны 90 см. Определим, каковы четыре низшие частоты, извлекаемые на такой струне?

Скорость волны на струне равна

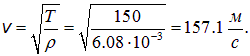
Наибольшая длина стоячей волны в струне равна  м. Отсюда находим самую низкую частоту:

(Эта частота соответствует ноте «фа» большой октавы.)

Следующие частоты являются целыми кратными n₁:

Отсюда следует: n₁ = 2·87.3 = 174.6 Гц («фа» малой октавы), n₃ = 3·87.3 = 261.9 Гц («до» первой октавы) и n₁ = 4·87.3 = 349.2 Гц («фа» первой октавы).

Пример 4. Струна звучит на ноте «до» первой октавы. Максимальное отклонение точек струны от положения равновесия равно и_тах = 2 мм. Найдем максимальную скорость и ускорение точек струны.

Закон колебания струны имеет вид (ср. (2.53)):

откуда находим скорость и ускорение точек струны:

По условию  (см. пример 3.). Максимальные значения скорости и ускорения равны:

 

Сложение гармоник

Выше мы уже занимались сложением колебаний, и теперь нам предстоит проделать то же самое, но для каждой точки колеблющейся струны.

Движение струны при возбуждении основной (первой) гармоники, показано на рис. 2.10–1. В начальном положении (линия отмечена красным цветом) точки струны имеют максимальное отклонение от положения равновесия. Под действием силы упругости они начинают двигаться (на рисунке – вертикально вниз), и форма струны через 1/8 периода показана линией зеленого цвета. Через четверть периода струна приходит в положение равновесия (линия черного цвета), но ее элементы имеют некоторые скорости, и потому в положении равновесия не задерживаются. Еще через 1/16 периода они оказываются в положении, показанном линией синего цвета, а через половину периода струна снова приобретает максимальное отклонение (пунктирная линия красного цвета), но в другую сторону, после чего процесс повторяется в обратном направлении. Так происходит колебание в стоячей волне, соответствующее первой гармонике, частоту которой мы обозначаем n₁.

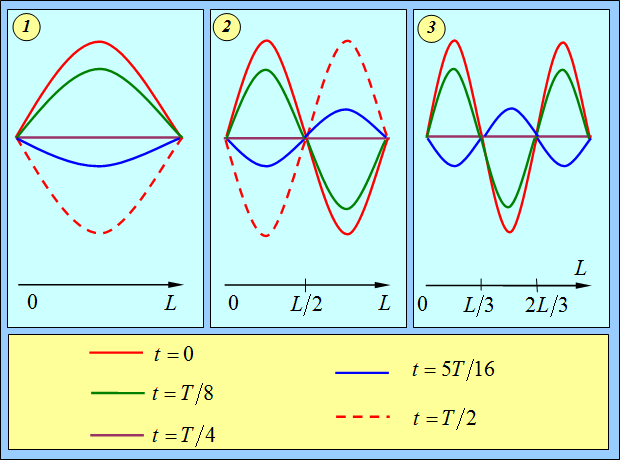
Рис. 2.10. Колебания струны:
1 –  первая гармоника; 2 –  вторая гармоника; 3 –  третья гармоника;

Но на струне, как мы уже знаем, могут возникать колебания и других гармоник. Вторая гармоника показана на том же рис. 2.10–2. Использование тех же обозначений позволяет не описывать процесс колебаний столь же детально. Заметим, что в этом случае имеется одна неподвижная точка (ее называют узлом) в середине струны. Поскольку узел все равно не движется, можно представить себе, что мы закрепили среднюю точку. И тем самым, не изменив частоты издаваемого звука, в два раза укоротили струну. Стало быть, частота колебаний ровно в два раза превышает частоту основной гармоники: . Этот результат мы уже получали другим способом.

На рис. 2.10–3 показаны колебания той же струны при возбуждении третьей гармоники. Здесь уже существует два узла, и издаваемый звук соответствует основному колебанию струны, укороченной в три раза (или, что то же самое, второй гармонике струны, длина которой составляет 2/3 исходной): .

Колебания струны для первых трех гармоник показаны на рис. 2.11. 

Рис. 2.11. Колебания струны для первых трех гармоник

На обсуждавшихся рисунках гармоники показаны без учета их амплитуд, то есть без учета их относительного вклада. На самом деле вклад гармоник может быть различным, так что в общем случае результирующее колебание получается сложением всех гармоник, каждая из которых представлена уравнением, аналогичным (2.59):

Здесь мы уже учли, что частоты и волновые числа принимают дискретный ряд значений; коэффициенты  – это амплитуды соответствующих гармоник. Заметим, что в множителе с зависимостью от времени мы заменили синус косинусом, то есть сдвинули точку отсчета времени. Теперь в момент t = 0 скорости всех точек струны равны нулю.

На практике приходится решать обратную задачу: находить коэффициенты  по известному результирующему колебанию. Численные значения  зависят от способа возбуждения струны, например, от ее начальной формы . Если нам задана функция , то для нее из (2.62) следует разложение:

которое известно в математике как разложение в ряд Фурье. Там же доказывается теорема, что коэффициенты и_п однозначно восстанавливаются по функции :

От величины примеси высших гармоник зависит форма колеблющейся струны. На рис. 2.12 показан вид колеблющейся струны в разные моменты времени при двух способах ее возбуждения. В обоих случаях струне придается некая начальная форма, после чего она отпускается «на свободу» (оставаясь закрепленной на концах, разумеется).

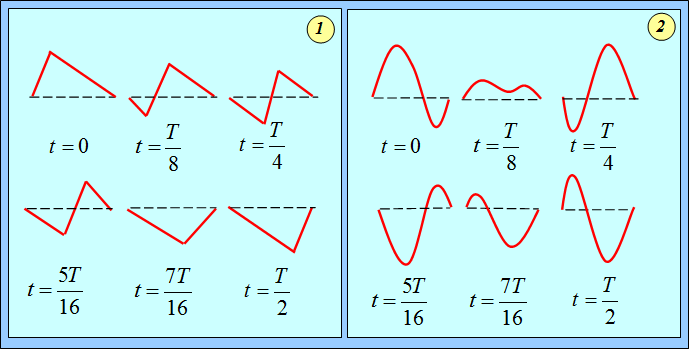
Рис. 2.12. Форма колеблющейся струны в различные моменты времени при разных формах струны в начальном состоянии:
1 –  струна оттянута на расстоянии 0.1 ее длины; 2 –  струне придана кусочно-синусоидная форма.

Мы рассматриваем два случая:

• в начальном положении струна оттягивается за точку, находящуюся на расстоянии 0.1 ее длины, считая от ее закрепленного конца;
• начальная форма струны описывается двумя синусоидами

Второй пример носит явно модельный характер и дан для сравнения. Надо сказать, что придание струне какой-то начальной формы — не единственный способ возбуждения колебаний. Можно, например, задать начальное распределение скоростей (как происходит, скажем, в фортепиано, где молоточек ударяет по струне, находящейся в положении равновесия).

Мы все же ограничимся двумя описанными случаями. На рис. 22.6 показаны положения точек струны за половину периода колебаний основной гармоники, после чего процесс повторяется в обратном направлении. За время, равное периоду колебаний Т₁ первой гармоники, струна возвращается в исходное положение. Если струна настроена на ноту «до» первой октавы, то Т₁ = 3.82 мс.