7.5. Гироскопы
Гироскопом называется массивное осесимметричное тело (симметричный волчок), быстро вращающееся вокруг оси симметрии, причем ось вращения может изменять положение в пространстве. Ось симметрии называется осью фигуры гироскопа.
Видео 7.6. Что же такое гироскоп?
Рис. 7.17. Движение системы гироскопов
Ось симметрии является одной из главных осей гироскопа. Поэтому его момент импульса совпадает по направлению с осью вращения.
Для того, чтобы изменить положение в пространстве положение оси фигуры гироскопа, необходимо подействовать на него моментом внешних сил.
Видео 7.7. Гироскопические силы:большой гироскоп рвет веревку
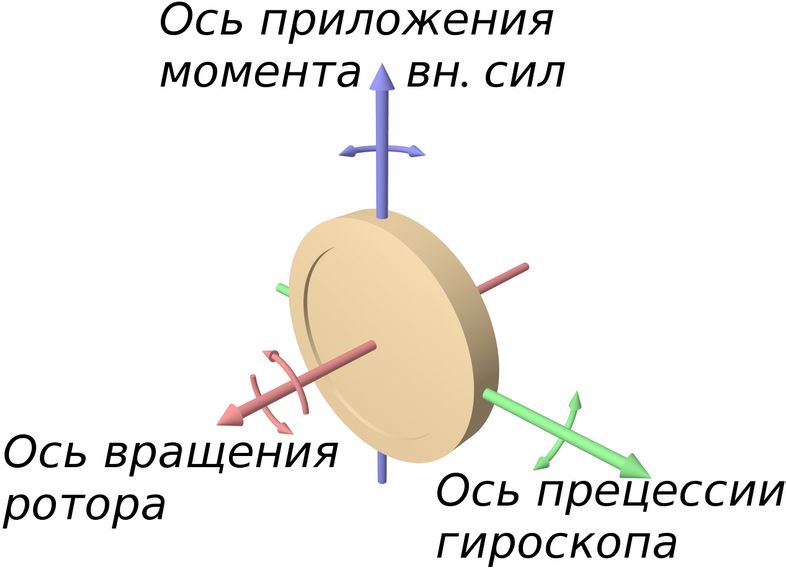
Рис. 7.18. Направление векторов при вращении гироскопа
При этом наблюдается явление, получившее название гироскопического: под действием сил, которые, казалось бы, должны были вызвать поворот оси 1 вокруг оси 2 (рис. 7.19), наблюдается поворот оси фигуры вокруг оси 3.
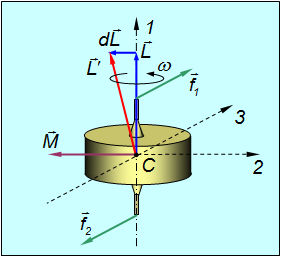
Рис. 7.19. Движение оси фигуры гироскопа под действием момента внешних сил
Видео 7.8. Гироскоп с перегрузами: направление и скорость прецессии, нутации
Гироскопические явления проявляются всюду, где имеются быстро вращающиеся тела, ось которых может поворачиваться в пространстве.
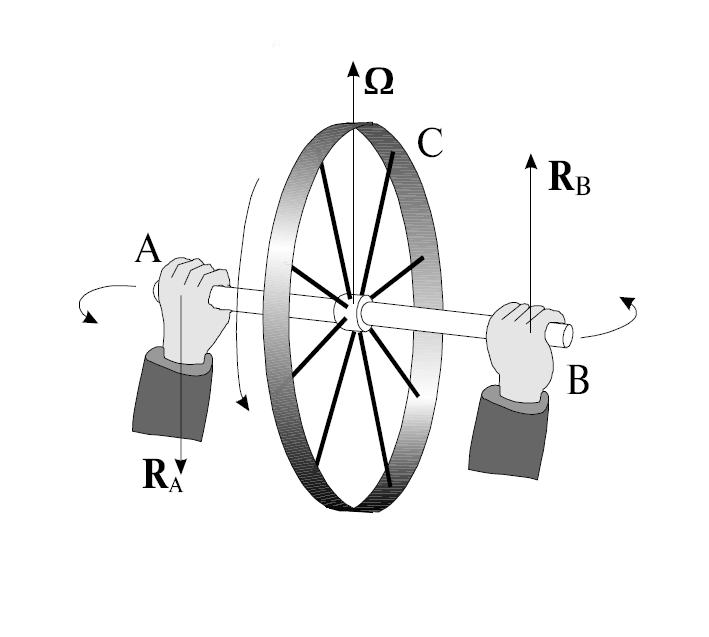
Рис. 7.20. Реакция гироскопа на внешнее воздействие
Странное на первый взгляд поведение гироскопа, рис. 7.19 и 7.20, полностью объясняется уравнением динамики вращательного движения твердого тела
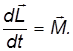
Видео 7.9. «Любвеобильный» гироскоп: ось гироскопа бежит вдоль направляющей, не покидая её
Видео 7.10. Действие момента силы трения: «Колумбово» яйцо
Если гироскоп привести в быстрое вращение, он будет обладать значительным моментом импульса. Если на гироскоп будет действовать внешняя сила в течение времени 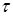 , то приращение момента импульса будет
, то приращение момента импульса будет
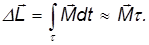
Если сила действует в течение короткого времени 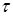 , то
, то
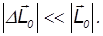
Другими словами, при коротких воздействиях (толчках) момент импульса гироскопа практически не меняется. С этим связана замечательная устойчивость гироскопа по отношению к внешним воздействиям, которая используется в различных приборах, таких как гирокомпасы, гиростабилизированные платформы и т. д.
Видео 7.11. Модель гирокомпаса, гиростабилизация
Видео 7.12. Большой гирокомпас

7.21. Гиростабилизатор орбитальной станции
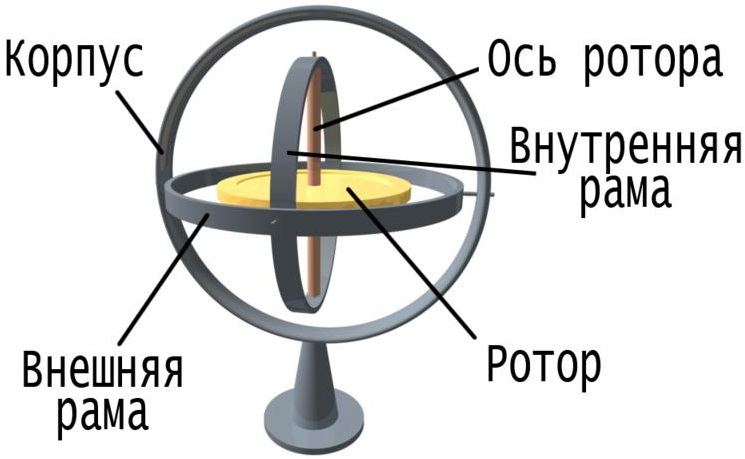
В гироскопах, применяющихся в авиации и космонавтике, используется карданов подвес, который позволяет сохранять направление оси вращения гироскопа независимо от ориентации самого подвеса:
Видео 7.13. Гироскопы в цирке: езда на одном колесе по проволоке
Дополнительная информация
http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 245–249 (§ 47): кинематическая теорема Эйлера о вращениях твердого тела вокруг неподвижной точки.
Рассмотрим движение гироскопа с неподвижной точкой опоры, как показано на на рис. 7.22.
Движение гироскопа под действием внешней силы называется вынужденной прецессией.
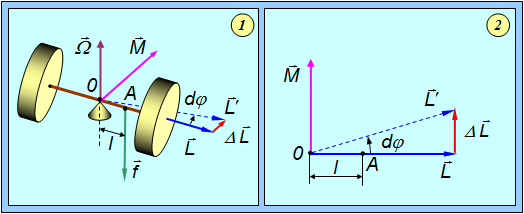
Рис. 7.22. Вынужденная прецессия гироскопа: 1 — общий вид; 2 — вид сверху
Приложим в точке А силу 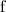 . Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы
. Если гироскоп не вращается, то, естественно, правый маховик будет опускаться, а левый — подниматься. Другая ситуация будет, если предварительно гироскоп привести в быстрое вращение. В этом случае под действием силы 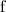 ось гироскопа будет вращаться с угловой скоростью
ось гироскопа будет вращаться с угловой скоростью  вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.
вокруг вертикальной оси. То есть ось гироскопа приобретает скорость в направлении, перпендикулярном направлению действующей силы.
Таким образом, прецессия гироскопа представляет собой движение под действием внешних сил, происходящее таким образом, что ось фигуры описывает коническую поверхность.
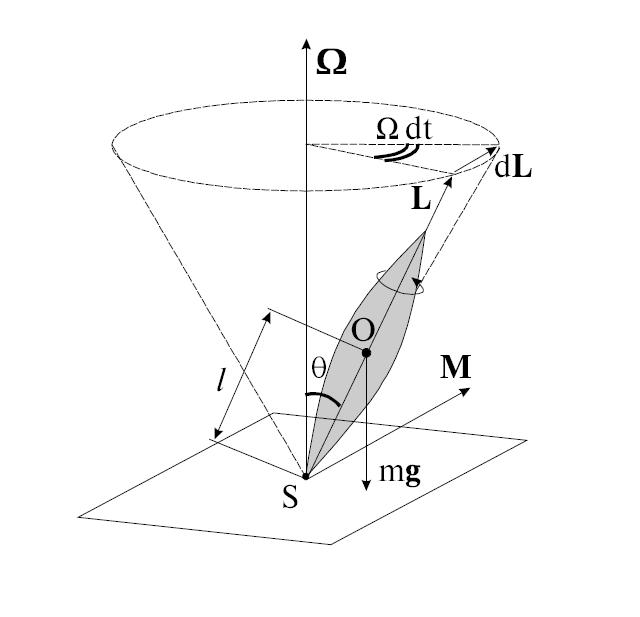
Рис. 7.23. К выводу формулы прецессии гироскопа.
Объяснение этого явления заключается в следующем. Момент силы  относительно точки 0 будет
относительно точки 0 будет
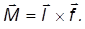
Приращение момента импульса гироскопа за время 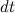 равно
равно
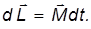
Это приращение перпендикулярно моменту импульса и, следовательно, меняет его направление, но не величину.
Вектор момента импульса ведет себя подобно вектору скорости при движении частицы по окружности. В последнем случае приращения скорости 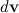 перпендикулярно скорости частицы
перпендикулярно скорости частицы 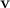 и равно по модулю
и равно по модулю
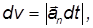
где
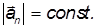
В случае гироскопа элементарное приращение момента импульса
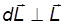
и равно по модулю
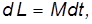
причем
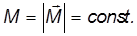
За время 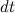 вектор момента импульса повернется на угол
вектор момента импульса повернется на угол 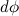
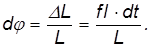
Угловая скорость вращения плоскости, проходящей через ось конуса, описываемого осью фигуры, и ось фигуры, называется угловой скоростью прецессии гироскопа.
Возникающие при определенных условиях колебания оси фигуры гироскопа в плоскости, проходящей через ось указанного выше конуса и саму ось фигуры, называются нутациями. Нутации могут быть вызваны, например, коротким толчком оси фигуры гироскопа вверх или вниз (см. рис. 7.24):

Рис. 7.24. Нутации гироскопа
Угловая скорость прецессии в рассматриваемом случае равна
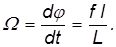
Отметим важное свойство гироскопа — его безынерционность, заключающееся в том, что после прекращения действия внешней силы вращение оси фигуры прекращается.
Дополнительная информация
http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 288–293 (§ 52): изложены основы точной теории гироскопа.
http://femto.com.ua/articles/part_1/0796.html — физическая энциклопедия. Описаны разнообразные механические гироскопы, которые используются для навигации — гирокомпасы.
http://femto.com.ua/articles/part_1/1901.html — физическая энциклопедия. Описан лазерный гироскоп для целей космической навигации.
Влияние гироскопических сил в технике иллюстрируется следующими рисунками.
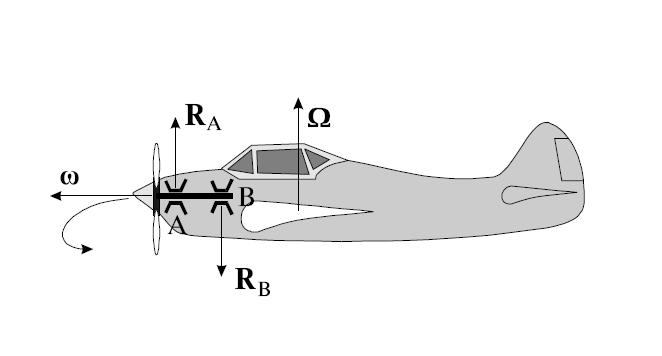
Рис. 7.25. Гироскопические силы,действующие на самолет при вращении винта
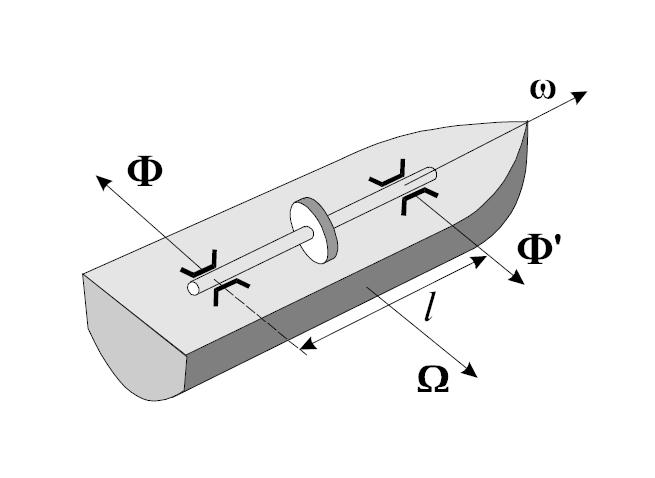
Рис. 7.26. Перевертывание волчка под действием гироскопических сил
Рис. 7.27. Как поставить яйцо «на попа»
Дополнительная информация
http://kvant.mirror1.mccme.ru/1971/10/mehanika_vrashchayushchegosya.htm — журнал «Квант» — механика волчка (С. Кривошлыков).
http://www.pereplet.ru/nauka/Soros/pdf/9809_096.pdf — Соросовский образовательный журнал, 1998 г., № 9, — в статье обсуждаются проблемы динамики вращающихся тел (кельтских камней), соприкасающихся с твердой поверхностью (А.П. Маркеев).
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_35.djvu — Михайлов А.А. Земля и ее вращение, Библиотечка Квант, выпуск 35 стр. 50–56 — планета Земля — большой волчок, ее ось прецессирует в пространстве.
Приложение
О принципе работы колеса
Раз уж мы много говорили в этой главе о вращении тел, остановимся на самом великом и важном открытии человечества — изобретении колеса. Всем известно, что волочить груз гораздо труднее, чем перевозить его на колесах. Встает вопрос, почему? Колесо, играющее огромную роль в современной технике, по праву считается одним из гениальнейших изобретений человечества.
Передвижение груза с помощью катка. Прототипом колеса был каток, подкладываемый под груз. Его первые применения теряются во мгле веков. Прежде чем разбираться с колесом, поймем принцип действия катка. Для этого рассмотрим пример.
Пример. Груз массой M положен на цилиндрический каток массой 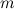 и радиусом
и радиусом  , который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила
, который может двигаться по плоскому горизонтальному настилу. К грузу приложена горизонтальная сила 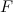 (рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.
(рис. 7.28). Найдем ускорения груза и катка. Силой трения качения пренебречь. Считать, что движение системы происходит без проскальзывания.
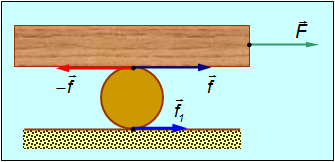
Рис. 7.28. Передвижение груза с помощью катка
Обозначим 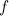 силу трения между катком и грузом и
силу трения между катком и грузом и 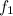 — между катком и настилом. За положительное направление примем направление внешней силы
— между катком и настилом. За положительное направление примем направление внешней силы 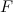 . Тогда положительным значениям
. Тогда положительным значениям 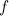 и
и 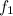 соответствуют направления сил трения, показанные на рис. 7.28.
соответствуют направления сил трения, показанные на рис. 7.28.
Таким образом, на груз действуют силы 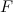 и
и 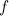 , а на каток — силы
, а на каток — силы 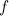 и
и 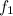 . Обозначим a ускорение груза и a1 — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением
. Обозначим a ускорение груза и a1 — ускорение катка. Кроме того, каток вращается по часовой стрелке с угловым ускорением  .
.
Уравнения поступательного движения принимают вид:
- для груза
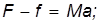
- для катка
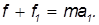
Уравнение вращательного движения катка записывается так:
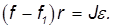
Обратимся теперь к условиям отсутствия проскальзывания. Из-за вращения катка его нижняя точка имеет линейное ускорение 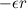 и, кроме того, участвует в поступательном движении с ускорением
и, кроме того, участвует в поступательном движении с ускорением 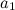 . В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что
. В отсутствие проскальзывания между катком и настилом полное ускорение нижней точки катка должно быть равно нулю, так что
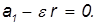
Верхняя точка катка приобретает из-за вращения противоположно направленное линейное ускорение 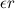 и то же ускорение
и то же ускорение 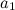 поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:
поступательного движения. Чтобы не было проскальзывания между катком и грузом, полное ускорение верхней точки должно быть равно ускорению груза:
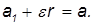
Из полученных уравнений для ускорений следует, что ускорение катка в два раза меньше ускорения груза:
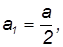
и, соответственно,
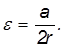
Из непосредственного опыта каждый знает, что каток действительно отстает от груза.
Подставляя соотношения для ускорений в уравнения движения и решая их относительно неизвестных  ,
, 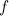 ,
, 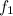 , получаем следующие выражение для ускорения груза
, получаем следующие выражение для ускорения груза
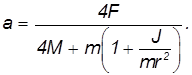
Обе силы трения 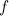 и
и 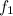 оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:
оказываются при этом положительными, так что на рис. 12 их направления выбраны правильно:
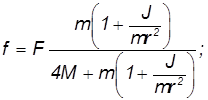
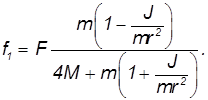
Как видно, радиус катка особой роли не играет: отношение 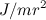 зависит только от его формы. При данных массе
зависит только от его формы. При данных массе 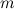 и радиусе
и радиусе  момент инерции катка максимален, когда каток представляет собой трубу:
момент инерции катка максимален, когда каток представляет собой трубу: 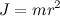 . В этом случае сила трения между катком и настилом отсутствует (
. В этом случае сила трения между катком и настилом отсутствует (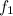 = 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:
= 0) а уравнения для ускорения груза и силы трения между грузом и катком принимают вид:
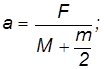
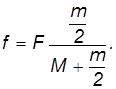
При уменьшении массы катка сила трения уменьшается, ускорение груза увеличивается — груз легче перемещать.
В случае катка-цилиндра (бревна)  /2 и мы находим силы трения
/2 и мы находим силы трения
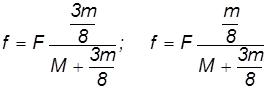
и ускорение груза.
Сравнивая с результатами для катка-трубы, видим, что эффективно масса катка как бы уменьшилась: ускорение груза возрастает при прочих равных условиях.
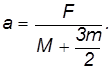
Главный итог рассмотренного примера: ускорение отлично от нуля (то есть груз начинает двигаться) при сколь угодно малой внешней силе. При волочении же груза по настилу для его смещения необходимо приложить как минимум силу 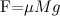 .
.
Второй вывод: ускорение вовсе не зависит от величины трения между частями данной системы. Коэффициент трения 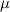 не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила
не вошел в найденные решения, он появится только в условиях отсутствия проскальзывания, которые сводятся к тому, что приложенная сила 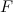 не должна быть слишком велика.
не должна быть слишком велика.
Полученный результат, что каток как бы полностью «уничтожает» силу трения, не удивителен. Действительно, в отсутствие относительного перемещения соприкасающихся поверхностей силы трения не совершают работы. На самом деле каток «заменяет» трение скольжения на трение качения, которым мы пренебрегли. В реальном случае минимальная сила, необходимая для движения системы, отлична от нуля, хотя и гораздо меньше, чем при волочении груза по настилу. В современной технике принцип действия катка реализуется в шарикоподшипниках.
Качественное рассмотрение работы колеса. Разобравшись с катком, перейдем к колесу. Первое колесо в виде деревянного диска, насаженного на ось, появилось, по-видимому, в IV тысячелетии до н.э. в цивилизациях Древнего Востока. Во II тыс. до н.э. конструкция колеса совершенствуется: появляются спицы, ступица и гнутый обод. Изобретение колеса дало гигантский толчок развитию ремесел и транспорта. Однако многие не понимают самого принципа действия колеса. В ряде учебников и энциклопедий можно найти неверное утверждение, что колесо, подобно катку, также дает выигрыш, заменяя силу трения скольжения на силу трения качения. Иногда приходится слышать ссылки на использование смазки или подшипников, но дело не в этом, поскольку колесо с очевидностью появилось раньше, чем додумались до смазки (и, тем более, подшипников).
Действие колеса проще всего понять, исходя из энергетических соображений. Древние повозки устроены просто: кузов прикрепляется к деревянной оси радиусом  (общая масса кузова с осью равна M). На ось насаживаются колеса массой
(общая масса кузова с осью равна M). На ось насаживаются колеса массой 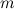 и радиусом R (рис. 7.29).
и радиусом R (рис. 7.29).
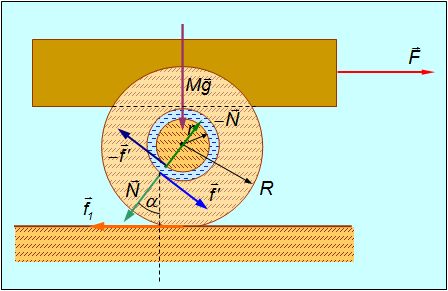
Рис. 7.29. Передвижение движение груза с помощью колеса
Предположим, что такую повозку везут по деревянному же настилу (тогда во всех соприкасающихся местах имеем тот же коэффициент трения 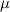 ). Сначала заклиним колеса и, действуя силой
). Сначала заклиним колеса и, действуя силой 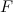 , протащим повозку на расстояние s. Поскольку повозка скользит по настилу, сила трения достигает своего максимально возможного значения
, протащим повозку на расстояние s. Поскольку повозка скользит по настилу, сила трения достигает своего максимально возможного значения
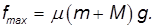
Работа против этой силы равна
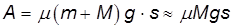
(так как обычно масса колес много меньше массы повозки 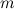 <<M).
<<M).
Освободим теперь колеса и снова протащим повозку на то же расстояние s. Если колеса не скользят по настилу, то в нижней точке колеса сила трения не совершает работы. Но трение скольжения возникает между осью и колесом в нижней части оси радиусом  . Там тоже имеется сила нормального давления. Она будет несколько отличаться от прежней за счет веса колес и других причин, которые мы обсудим ниже, но при небольшой массе колес и небольшом коэффициенте трения можно считать ее примерно равной
. Там тоже имеется сила нормального давления. Она будет несколько отличаться от прежней за счет веса колес и других причин, которые мы обсудим ниже, но при небольшой массе колес и небольшом коэффициенте трения можно считать ее примерно равной  . Поэтому между осью и колесом действует та же самая сила трения
. Поэтому между осью и колесом действует та же самая сила трения

Подчеркнем еще раз: колесо само по себе не уменьшает силу трения. Но работа A' против этой силы будет теперь гораздо меньше, чем в случае волочения повозки с заклиненными колесами. Действительно, когда повозка проходит расстояние S, ее колеса совершают  оборотов. Значит, трущиеся об ось колеса поверхности сдвинутся друг относительно друга на меньшее расстояние
оборотов. Значит, трущиеся об ось колеса поверхности сдвинутся друг относительно друга на меньшее расстояние  . Поэтому работа против сил трения также будет в соответствующее число раз меньше:
. Поэтому работа против сил трения также будет в соответствующее число раз меньше:

Таким образом, надев колеса на оси, мы уменьшаем не силу трения, как в случае с катком, а путь, на котором она действует. Скажем, колесо радиусом R = 0,5 м и осью радиусом  = 2 см уменьшает работу на 96 %. С остальными 4 % успешно справляются смазка и подшипники, уменьшающие само трение (смазка, кроме того, предотвращает износ ходовой части повозки). Теперь понятно, почему в старых экипажах и боевых колесницах делали такие большие колеса. Современные продуктовые коляски в супермаркетах могут катиться лишь благодаря подшипникам.
= 2 см уменьшает работу на 96 %. С остальными 4 % успешно справляются смазка и подшипники, уменьшающие само трение (смазка, кроме того, предотвращает износ ходовой части повозки). Теперь понятно, почему в старых экипажах и боевых колесницах делали такие большие колеса. Современные продуктовые коляски в супермаркетах могут катиться лишь благодаря подшипникам.
Из полученной формулы для работы при качении следует, что при  = R (колеса без оси, вмонтированные в корпус и трущиеся об него) будет совершена та же работа, что и при волочении повозки. Весь выигрыш заключен в отношении радиусов
= R (колеса без оси, вмонтированные в корпус и трущиеся об него) будет совершена та же работа, что и при волочении повозки. Весь выигрыш заключен в отношении радиусов  /R, то есть колесо — по сути дела рычаг непрерывного действия с плечами
/R, то есть колесо — по сути дела рычаг непрерывного действия с плечами  и R. Благодаря «сворачиванию» рычага в окружность его не надо возвращать в начальное положение: это достигается автоматически. Трудно представить себе техническое изобретение, более гениальное по простоте и эффективности!
и R. Благодаря «сворачиванию» рычага в окружность его не надо возвращать в начальное положение: это достигается автоматически. Трудно представить себе техническое изобретение, более гениальное по простоте и эффективности!
Количественная теория колеса. Рассмотрим силы, действующие на нашу повозку (см. рис. 7.29).
Силы, действующие на колесо: сила трения  со стороны оси, сила нормального давления
со стороны оси, сила нормального давления  со стороны оси, сила трения
со стороны оси, сила трения 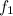 со стороны настила. Эти силы показаны на рис. 7.29 соответственно синей, зеленой и оранжевой стрелками. Заметим, что мы не предполагаем, что ось соприкасается с колесом в своей нижней точке: угол
со стороны настила. Эти силы показаны на рис. 7.29 соответственно синей, зеленой и оранжевой стрелками. Заметим, что мы не предполагаем, что ось соприкасается с колесом в своей нижней точке: угол  описывает смещение назад точки соприкосновения оси с колесом (соответственно, точки приложения сил
описывает смещение назад точки соприкосновения оси с колесом (соответственно, точки приложения сил  ,
,  ). Значение угла
). Значение угла  также должно быть найдено из решений уравнений движения. Кроме того, на колесо действует сила тяжести
также должно быть найдено из решений уравнений движения. Кроме того, на колесо действует сила тяжести  и нормальное давление
и нормальное давление  со стороны настила, но они сейчас нам не важны и на рисунке не показаны.
со стороны настила, но они сейчас нам не важны и на рисунке не показаны.
Выбирая ось х в горизонтальном направлении, а ось у — в вертикальном, записываем проекцию уравнения поступательного движения колеса на ось x :

Предполагая отсутствие проскальзывания в точке соприкосновения колеса с настилом (то есть  ), записываем уравнение вращательного движения колеса:
), записываем уравнение вращательного движения колеса:

Силы, действующие на повозку (показаны соответственно красной, фиолетовой, темно-синей и темно-зеленой стрелками на рис. 7.29): внешняя сила  , сила тяжести
, сила тяжести  и силы
и силы  ,
,  со стороны оси. Записываем уравнения поступательного движения повозки в проекциях на оси x, y :
со стороны оси. Записываем уравнения поступательного движения повозки в проекциях на оси x, y :

Мы имеем пять уравнений для пяти неизвестных:  ,
, 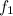 ,
,  ,
,  ,
,  . Их все можно найти, решая систему уравнений. Мы хотим получить лишь ответ на вопрос: при какой минимальной силе
. Их все можно найти, решая систему уравнений. Мы хотим получить лишь ответ на вопрос: при какой минимальной силе  повозка сдвинется с места? Для этого надо положить
повозка сдвинется с места? Для этого надо положить  , при этом ускорение
, при этом ускорение  = 0. Имеем тогда систему уравнений:
= 0. Имеем тогда систему уравнений:

Здесь мы уже учли выражение закона трения скольжения. Из двух первых уравнений следует:

откуда можно найти тригонометрические функции угла  :
:

Тогда из двух последних уравнений следует искомое выражение:

Любопытно, что масса колес не вошла в конечный ответ для  .
.
В предельном случае  = R имеем
= R имеем  , что соответствует, в сущности, отсутствию колес и перетаскивание повозки волоком. В обратном предельном случае
, что соответствует, в сущности, отсутствию колес и перетаскивание повозки волоком. В обратном предельном случае

минимальная сила также стремится к нулю. При малых коэффициентах трения квадратный корень в знаменателе приближенно равен единице, и

Выше мы качественно получили этот результат из энергетических соображений.
Дополнительная информация
http://kvant.mirror1.mccme.ru/1970/12/pochemu_ustojchiv_velosiped.html — Объяснение устойчивости велосипеда (Д. Джоунс).
http://kvant.mirror1.mccme.ru/1980/05/ustojchivost_avtomobilya.html — Журнал «Квант» — устойчивость езды на автомобиле (Л. Гродко).


