Групповой анализ дифференциальных уравнений
Лекция 4
Скачать
Национальный Исследовательский Ядерный
университет «МИФИ»
Кафедра Прикладной Математики

Николай А. Кудряшов

Групповой Анализ
Дифференциальных Уравнений


Лекции для Т8-31

Содержание 4-ой лекции

2.18 Алгебра Ли. Поалгебры Ли. Идеал
2.19 Метод интегрирования Софуса Ли ОДУ второго порядка
2.20 Пример интегрирования ОДУ второго порядка
2.21 Обыкновенные дифференциальные уравнения с заданной симметрией
2.22 Примеры обыкновенных дифференциальных уравнений с заданной симметрией

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Алгебра Ли. Поалгебры Ли. Идеал

Метод интегрирования Софуса Ли для ОДУ второго порядка

Метод интегрирования Софуса Ли для ОДУ второго порядка

Метод интегрирования Софуса Ли для ОДУ второго порядка

Метод интегрирования Софуса Ли для ОДУ второго порядка

Метод интегрирования Софуса Ли для ОДУ второго порядка

Метод интегрирования Софуса Ли для ОДУ второго порядка

Пример интегрирования ОДУ второго порядка

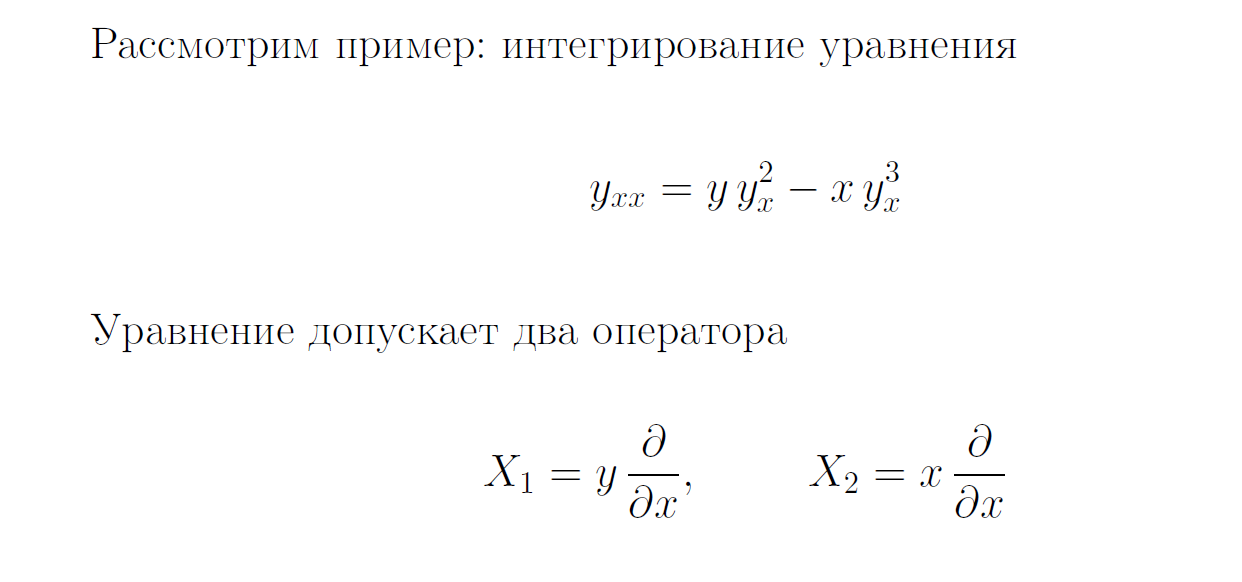
Пример интегрирования ОДУ второго порядка

Пример интегрирования ОДУ второго порядка

Пример интегрирования ОДУ второго порядка

Пример интегрирования ОДУ второго порядка

Уравнения с заданной симметрией

Уравнения с заданной симметрией

Уравнения с заданной симметрией

Примеры дифференциального уравнения с заданной симметрией

Примеры дифференциального уравнения с заданной симметрией

Уравнение с заданной симметрией

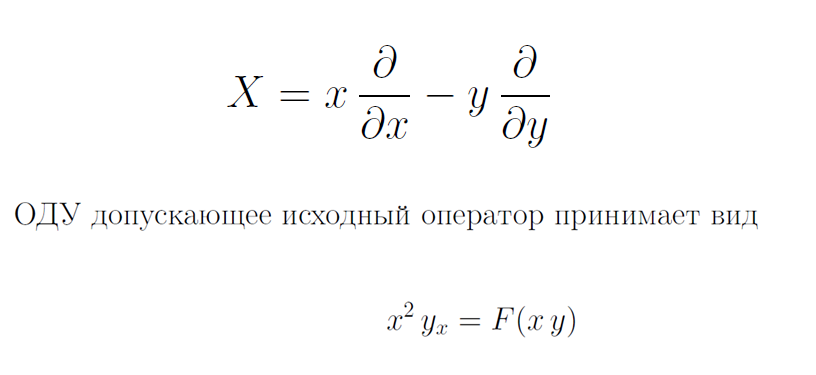
Примеры ОДУ 1-го порядка с заданной симметрией

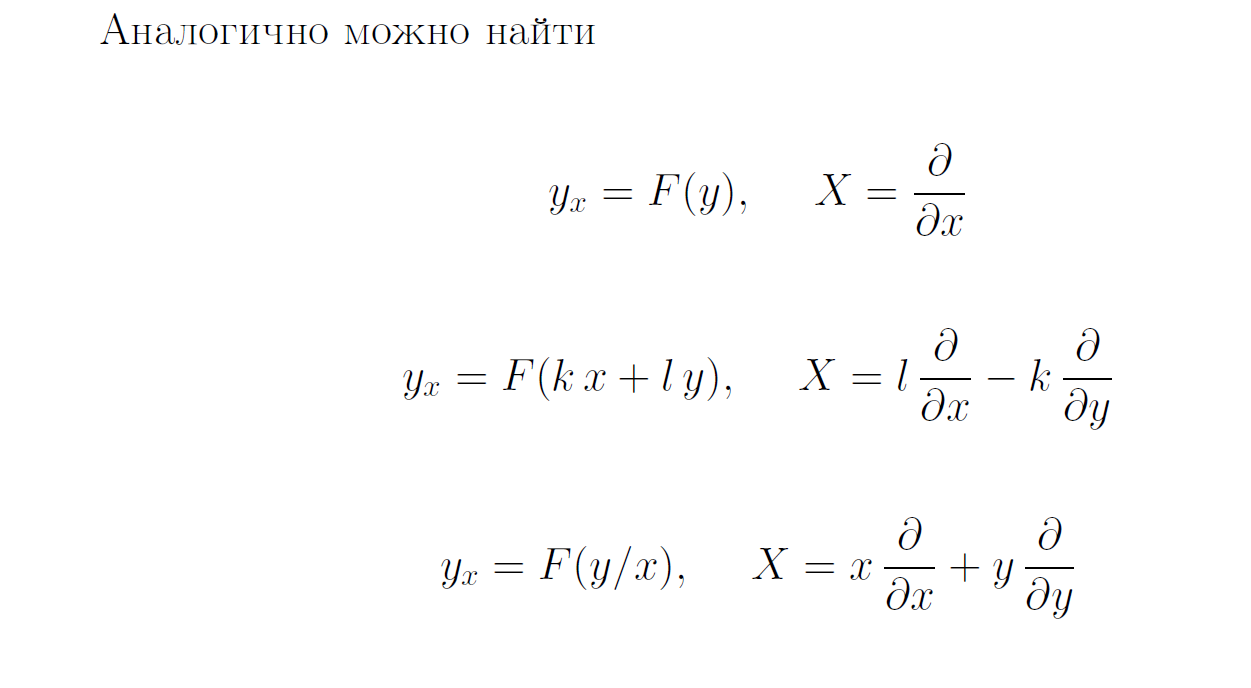
Примеры ОДУ с заданной симметрией

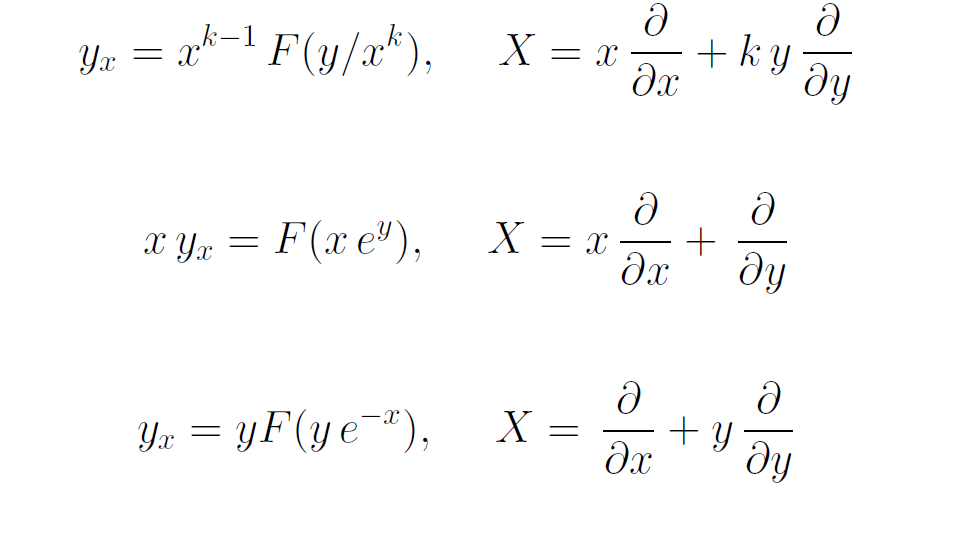
Примеры ОДУ с заданной симметрией

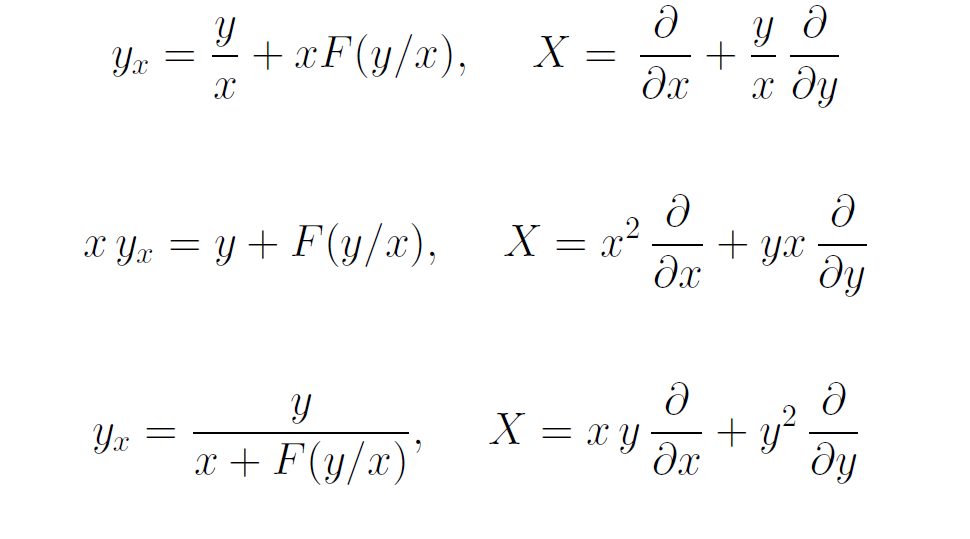
Примеры ОДУ с заданной симметрией

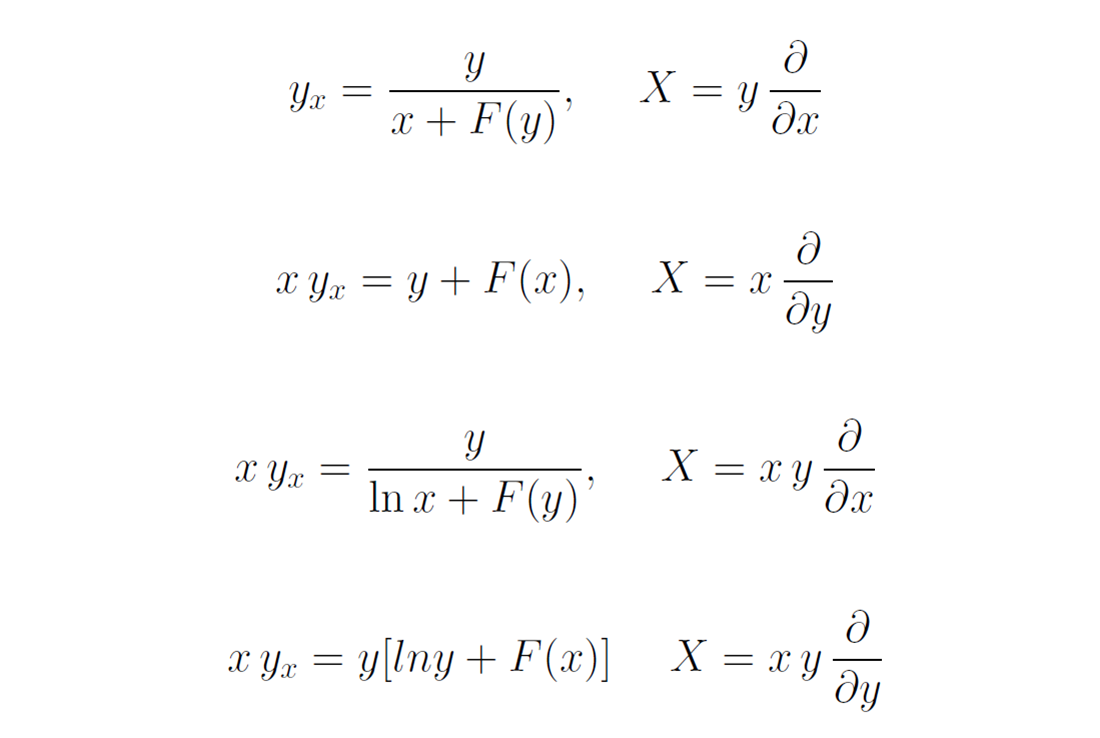
Литература

  • Кудряшов Н.А. Методы нелинейной математической физики, Из-во «Интеллект», Долгопрудный, 2010
  • Ибрагимов Н.Х., Практический курс дифференциальных уравнений и математического моделирования, Из-во Нижегородского государственного университета, 2007
  • Ибрагимов Н.Х. Азбука группового анализа, № 8, 1991, Из-во «Знание».
  • Ибрагимов Н.Х. Опыт группового анализа, №7, 1991, Из-во «Знание».