Форма Лагранжа

Пусть заданная функция имеет все производные до порядка n + 1 включительно в интервале (a − δ; a + δ), где δ > 0. Тогда существует точка ξ лежащая между точками x и a, что

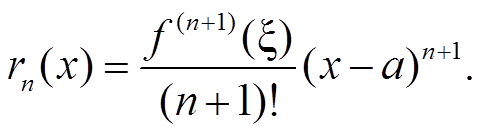
В формуле Шлемильха–Роша

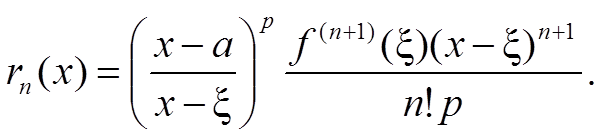
выберем p = n + 1. Получим формулу Лагранжа.