Теорема Коши

Следствие

Пусть функции f(x) и g(x) непрерывны на отрезке [a; b] и дифференцируемы в интервале (a; b), причем при всех x ∈ (a; b) производная g′(x) ≠ 0. Тогда для любых точек α, β ∈ (a, b) найдется точка ξ, лежащая между α и β (т. е. либо α ≤ ξ ≤ β, либо β ≤ ξ ≤ α), для которой

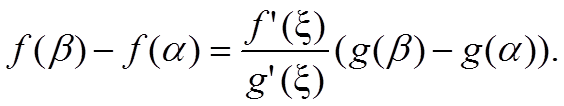
(1) α < β По теореме Коши для отрезка [a; b].

(2) α > β По теореме Коши для отрезка [b; a].

(3) α = β Обе части равенства равны нулю.

Контрпример

f(x) = x², g(x) = x³, a = –1, b = 1.

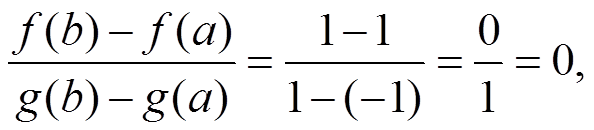
в то время как

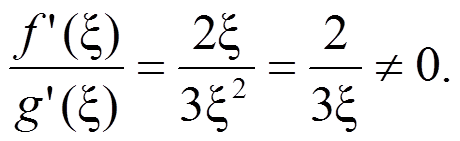
Условия теоремы Коши не выполнены: производная функции g(x) в интервале (–1; 1) обращается в нуль (в точке x = 0).