Монотонность

Условие монотонности дифференцируемой функции

Возрастающая функция: x₁ < x₂ ⇒ f(x₁) ≤ f(x₂).

Убывающая функция: x₁ < x₂ ⇒ f(x₁) ≥ f(x₂).

Дифференцируемая в интервале (a; b) функция f(x) возрастает тогда и только тогда, когда в этом интервале f ′ (x) ≥ 0.

Пусть f(x) возрастает, тогда для любой точки x₀ величина

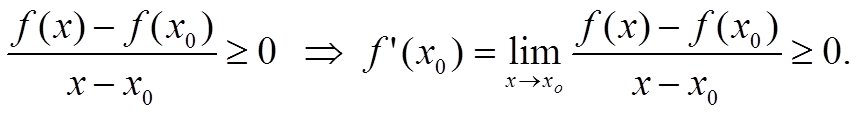
Обратно, пусть всюду f ′(x) ≥ 0 и x₁ < x₂. По формуле Лагранжа т. е.

f(x₁) − f(x₂) = f ′(ξ)(x₁ − x₂) ≤ 0   f(x₁) ≤ f(x₂)

Дифференцируемая в интервале (a; b) функция f(x) возрастает тогда и только тогда, когда в этом интервале f ′ (x) ≤ 0.