Выпуклость функции

Дифференцируемая в интервале (a; b) функция f(x) вогнута тогда и только тогда её производная убывает.

Функция f(x) вогнута тогда и только тогда, когда

g(x) = −f(x)

выпукла, т. е. g′(x) возрастает. Однако, это равносильно тому, что функция f ′(x) = −g′(x) убывает.

Дважды дифференцируемая в интервале (a; b) функция f(x) выпукла тогда и только тогда, когда всюду f ″(x) ≥ 0.

1) f ″ ≥ 0.

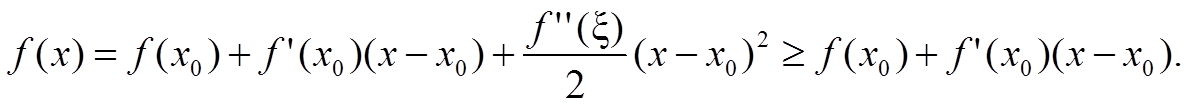
2) Функция выпукла.
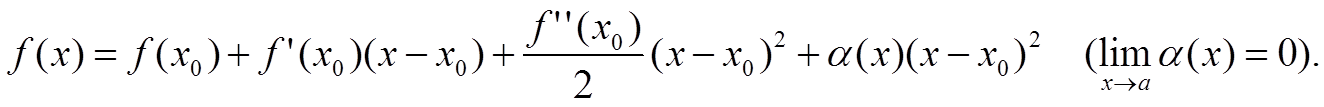
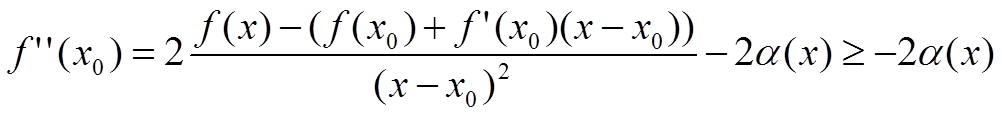