Кривизна плоской кривой

Теорема

Пусть на плоскости задана гладкая регулярная кривая

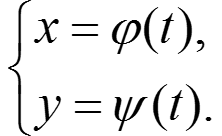
Тогда её кривизна в каждой точке t₀ определяется формулой

Замечание

Гладкая: φ, ψ ∈ C¹

Регулярная: |φ′ (t)|² + |ψ′ (t)|² ≠ 0

Доказательство

Так как кривая регулярна, то величина

|φ′ (t)|² + |ψ′ (t)|² ≠ 0

Пусть для определённости

φ′ (t) ≠ 0

Касательный вектор к кривой

Образует с осью абсцисс угол