Касательная к кривой

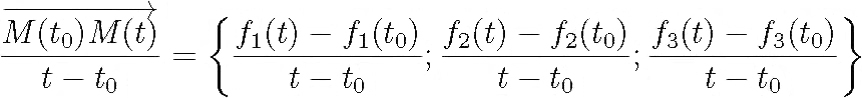
Предельное значение этого вектора при t → t₀

(в том случае, когда оно отлично от нулевого вектора) называется касательным вектором к кривой в точке t₀.

Прямая, проходящая через точку M(t₀) с этим направляющим вектором, называется касательной к кривой в точке t₀.

Особые и регулярные точки кривой

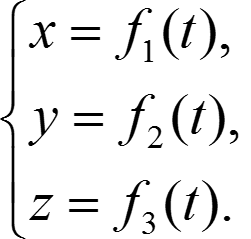
[f₁′(t)]² + [f₂′(t)]² +[f₃′(t)]² ≠ 0 — регулярная точка

[f₁′(t)]² + [f₂′(t)]² +[f₃′(t)]² = 0 — особая точка

В регулярной точке кривая всегда имеет касательную.