Теорема Лагранжа

Пусть функция f(x) непрерывна на отрезке [a; b] и дифференцируема в интервале (a; b). Тогда существует такая точка
ξ ∈ (a; b), что

Пусть

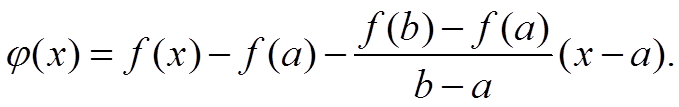
Эта функция удовлетворяет условиям теоремы Ролля и поэтому существует такая точка ξ ∈ (a; b) для которой φ′(ξ) = 0 т. е.

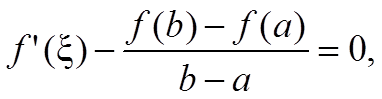
что доказывает теорему.

Формулу Лагранжа часто записывают в другой форме

f(b) − f(a) = f ′(ξ)(b − a).

Эту теорему называют также теоремой о конечных приращениях.