Теорема Коши
Пусть функции f(x) и g(x) непрерывны на отрезке [a; b] и дифференцируемы в интервале (a; b). Пусть также при всех
x ∈ (a; b) производная g′(x) ≠ 0.
Тогда существует такая точка ξ ∈ (a; b), для которой
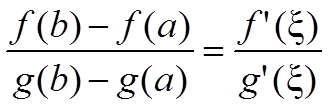
Прежде всего отметим, что g(b) ≠ g(a) так как в противном случае по теореме Ролля должна найтись точка, в которой
g′(x) = 0, а это противоречит условию теоремы. Рассмотрим далее вспомогательную функцию
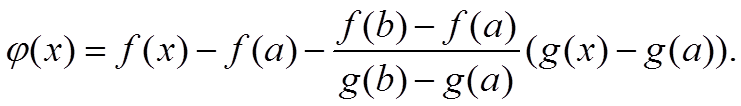
Эта функция удовлетворяет условиям теоремы Ролля, следовательно, существует такая точка ξ ∈ (a; b), в которой производная этой функции равна нулю
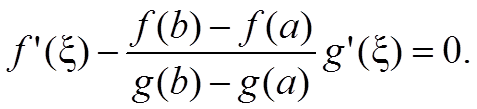
Так как по условию теоремы производная g′(x) ≠ 0, то из последнего равенства следует формула Коши.



