Lemma about the embedded segments. Mappings of sets

Lemma

If the segments [a_n; b_n] are embeded one in another, that is ∀ n[a_n; b_n] [a_n+1; b_n+1] , then there exists number c ∈ R, such that c ∈ [a_n; b_n], ∀ n

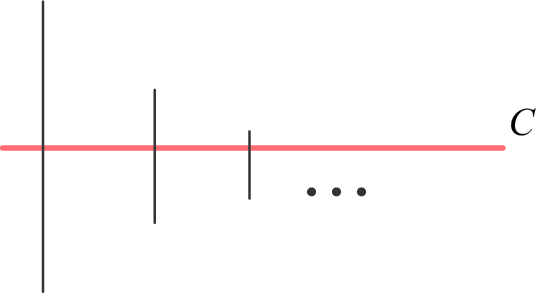
Proof

Y — the set of left bounds of segments, Z — the set of right bounds. According to axiom 5 of completeness, there exists
c ∈ R: a_n ≤ c ≤ b_m for any n and m. In particular for m = n.