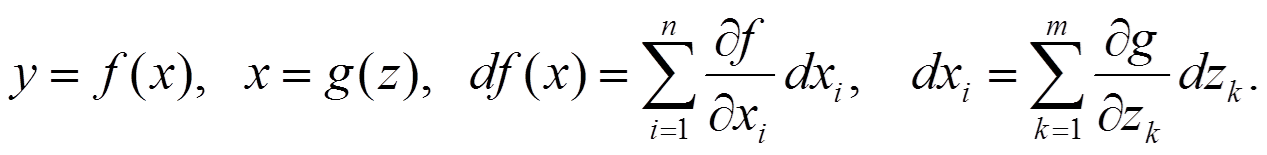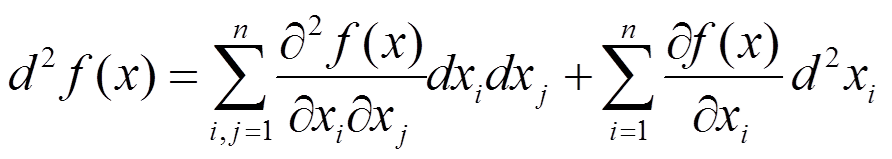Второй дифференциал сложной функции
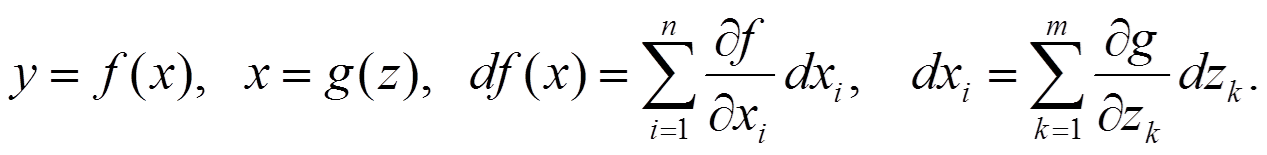
$$d^2f(x) = d \sum_{i=1}^{n} \frac{\partial f(x)}{\partial x_i}dx_i = \sum_{i=1}^{n} d \left ( \frac{\partial f(x)}{\partial x_i}dx_i \right ) = \sum_{i=1}^{n} \left [ d \left ( \frac{\partial f(x)}{\partial x_i} \right )dx_i + \frac{\partial f(x)}{\partial x_i} d(dx_i) \right ] = $$
$$\sum_{i=1}^{n} d \left ( \frac{\partial f(x)}{\partial x_i} \right )dx_i + \sum_{i=1}^{n} \frac{\partial f(x)}{\partial x_i} d(dx_i) = \sum_{i=1}^{n} \left ( \sum_{j=1}^{n} \frac{\partial}{\partial x_j} \left (\frac{\partial f(x)}{\partial x_i} \right ) dx_j \right ) dx_i + $$
$$+ \sum_{i=1}^{n} \frac{\partial f(x)}{\partial x_i} d^2x_i = \sum_{i,j=1}^{n} \frac{\partial^2 f(x)}{\partial x_i \partial x_j} dx_i dx_j + \sum_{i=1}^{n} \frac{\partial f(x)}{\partial x_i} d^2x_i$$
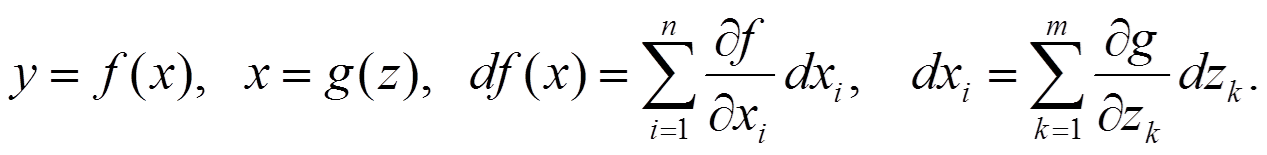
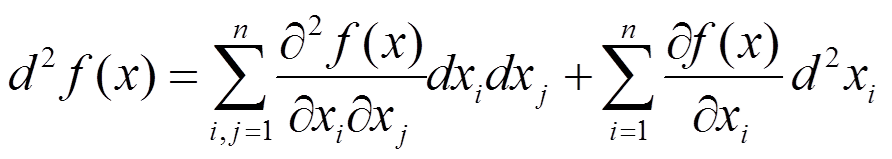

 Производные и дифференциалы неявных функций, производные и дифференциалы высших порядков. Формула Тейлора для функций нескольких переменных. Экстремум функций нескольких переменных
Производные и дифференциалы неявных функций, производные и дифференциалы высших порядков. Формула Тейлора для функций нескольких переменных. Экстремум функций нескольких переменных  Второй...
Второй...