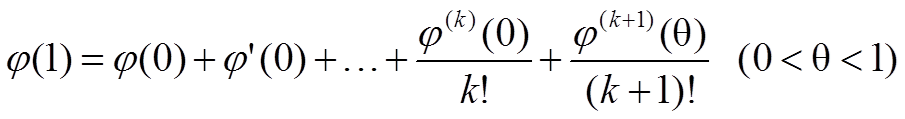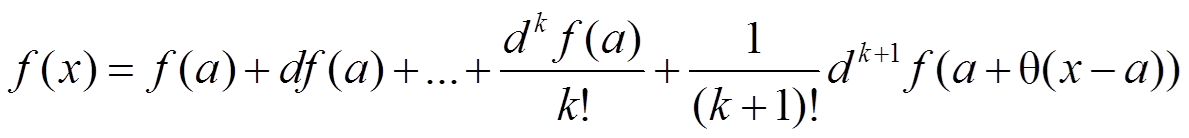Формула Тейлора

Рассмотрим вспомогательную функцию

φ(t) = f(a + t(x − a)).

Лемма

φ(t) = C^{k +1}[0; 1],   φ^(m)(t) = d^m f(a + t(x − a))   (0 ≤ m ≤ k + 1).

$$1) \varphi'(t) = \sum_{i=1}^{n} \frac{\partial f}{\partial x_i} \frac{dx_i}{dt} = \sum_{i=1}^{n} \frac{\partial f}{\partial x_i} (x_i - a_i) = \sum_{i=1}^{n} \frac{\partial f}{\partial x_i} dx_i = df(x+t(x-a))$$

2) Пусть φ^(s)(t) = d^sf(x + t(x − a)), тогда

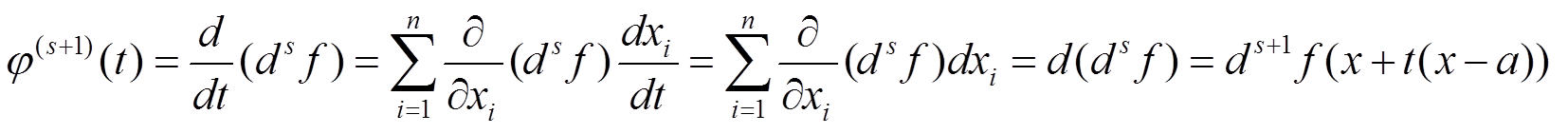
φ(t) = f(a + t(x − a))

φ^(m)(t) = d^mf(a + t(x − a))