Свойства определённого интеграла

Теорема о среднем для интеграла

Если функция y = f(x) непрерывна на отрезке [a; b], то существует число c ∈ [a; b] такое, что .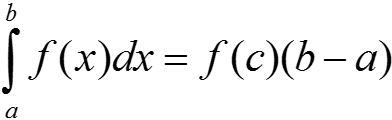

Доказательство

Из оценки → .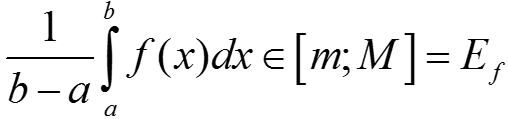

Оценка модуля интеграла

.

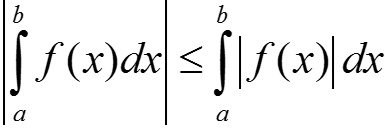Доказательство

.

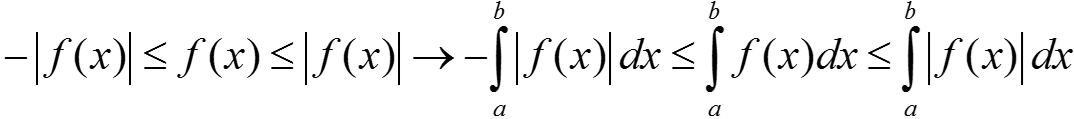Аддитивность интеграла по множеству

Если функция y = f(x) интегрируема на отрезках [a; c] и [c; b], то она интегрируема на их объединении и

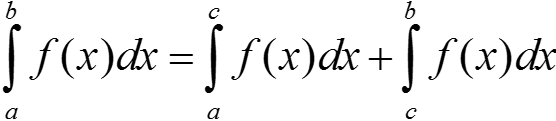
Замечание об интегрировании разрывных функций

Если функция имеет на отрезке [a; b] конечное число разрывов первого рода, то она интегрируема на [a; b]. Такие функции называются кусочно-непрерывными.