Основные определения, примеры

П.1

Понятие интеграла Римана

Разбиение τ = {x₀, x₁, …, x_n} отрезка [a, b] точками x₀ = a, x₁, x₂, …, x_n = b. Параметр разбиения
, где Δx_k = x_k − x_k−1.

Определение

Для любого набора ξ = {ξ₁, ξ₂, …, ξ_n} точек ξ_k ∈ [x_k−1; x_k] выражение называется интегральной суммой Римана.

Определение

Интегралом Римана функции y = f(x) на отрезке [a; b] называют число равное 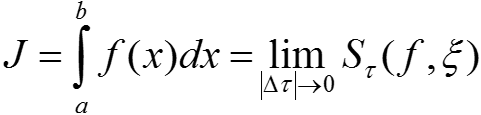, т. е.

∀ ε > 0 ∃ δ = δ_ε: ∀ τ,   |τ| < δ,   ∀ ξ → |S_τ(f, ξ) − J| < ε.