Формула Ньютона–Лейбница

Интеграл Римана можно вычислить по формуле:

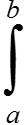f(x)dx = F_f (b) − F_f (a),

где F_f (x) — произвольная первообразная функции f(x).

Доказательство

F_f (x) = F(x) + c.

F(a) = 0.

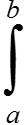f(t)dt = F(b) = F(b) − F(a) = (F_f (b) − c) − (F_f (a) − c) = F_f (b) − F_f (a).