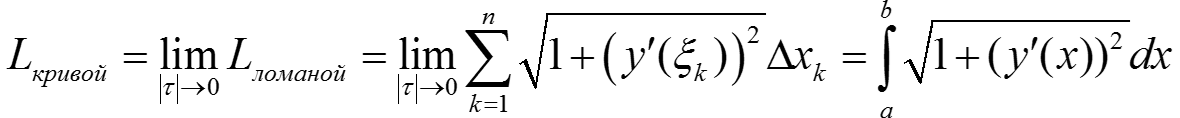Длина кривой, заданной параметрически
Понятие длины кривой:
|
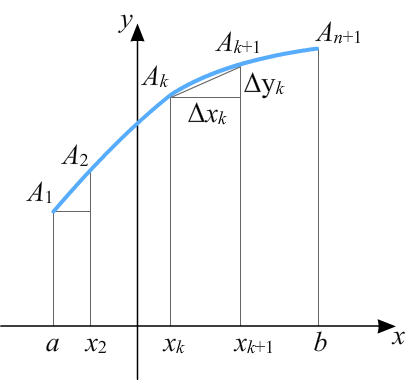
1. Ломаная, вписанная в кривую, и её длина:
2. Кривая задаётся графиком функции y = f(x), имеющей непрерывную производную на отрезке [a; b] $$L_{\textit{ломаной}} = \sum_{k=1}^{n} \sqrt{\Delta^2x_k + \Delta^2y_k} = \sum_{k=1}^{n} \sqrt{1 + \left ( \frac{\Delta y_k}{\Delta x_k} \right )^2} \Delta x_k = $$ $$\sum_{k=1}^{n} \sqrt{1 + \left ( y'(\xi_k) \right )^2} \Delta x_k,$$ где $$\xi_k \in \left [ x_k;x_{k+1} \right ].$$
|
|