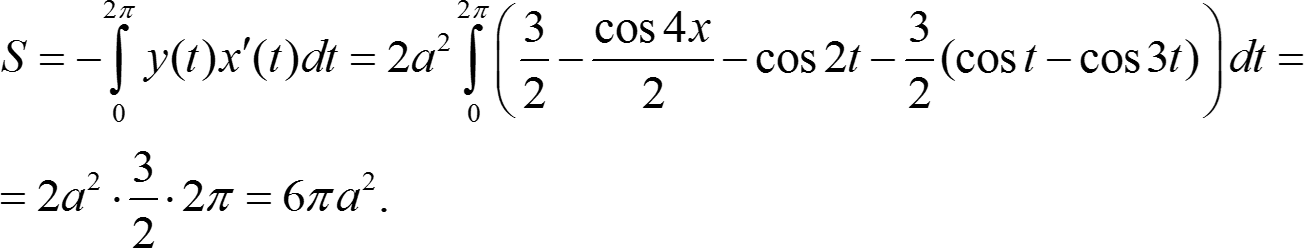Площадь фигуры в декартовой системе координат. Примеры

Пример 4

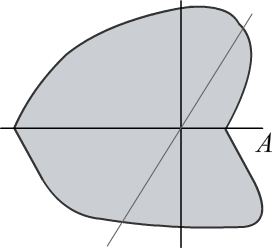
Вычислить площадь фигуры, ограниченной кривой:

x = a(2cos t − cos 2t), y = a(2sin t − sin 2t)

x′ = a(2sin 2t − 2sin t) → y(t)x′(t) = −2a2(sin2 2t + 2sin2 x − 3sin t sin 2t) = .

Условная картинка: T1 = 2π