Несобственные интегралы

Прежде чем переходить к понятию несобственного интеграла, необходимо вспомнить определение интеграла по Риману.

Интеграл по Риману

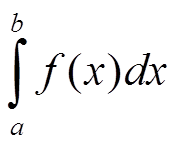
(или собственный интеграл) предполагает, что

1) a, b — конечные числа,

2) f(x) — ограничена на [a; b] (необходимое условие интегрируемости),

то есть область задачи ограничена отрезком [a; b] по оси Ox и отрезком [m; M] по оси Oy, где m = Inf f(x), M = Sup f(x), x ∈ [a; b].