Ряд Тейлора. Понятие. Историческая справка

Пусть функция f(x) имеет на интервале (a − R, a + R) (непрерывные) производные любого порядка.

Определение

Ряд где мы будем называть рядом Тейлора функции f(x).

(Считают по определению, что 0! = 1.)

Если f ⁽ⁿ⁾(a) понимать не как точное значение производной, а как предельное значение

то формула для ряда Тейлора годится и для многих не столь «хороших» функций. В остальных случаях ряд Тейлора сходится на своём интервале сходимости к функции f(x), то есть

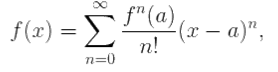   x ∈ (a − R, a + R).

К таким функциям относятся все элементарные функции — полиномы, e^x, sin x, cos x и т. п.)

Однако, есть примеры функций, чей ряд Тейлора сходится не к этим функциям.

Например, так как все произвольные функции в точке x = 0 равны нулю, то её ряд Тейлора сходится на к функции, равной тождественному нулю.

(При a = 0 ряд Тейлора часто называют рядом Маклорена)