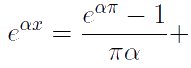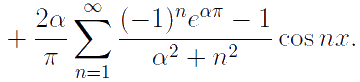Ряд Фурье «по синусам» и «по косинусам»

Таким образом, для функции f (x) = eαx на промежутке [0, π] имеем рsазложение по косинусам:

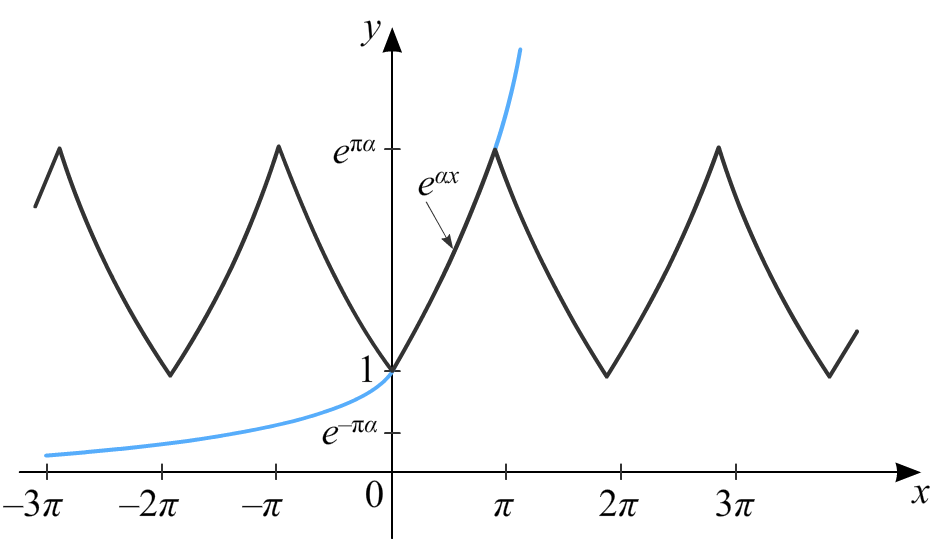
Надо отметить, что в двух последних примерах нами получены три различных представления одной и той же функции рядом Фурье. Что это означает? Во-первых: все эти ряды сходятся на интервале (0, π) к заданной функции f(x) = e^αx, во-вторых, за пределами интервала (0, π) их суммы ведут себя по-разному, при этом сумма ряда по синусам — нечётная 2π-периодическая функция, сумма ряда по косинусам — чётная 2π-периодическая функция, а сумма ряда по синусам и косинусам из первого примера 2π-периодическое продолжение функции f(x) = e^αx на всю числовую ось, совпадающее с f(x) на (−π, π).

Таким образом, три различных ряда Фурье сходятся к функциям, различным на , но совпадающим на (0, π) друг с другом и
с f(x).