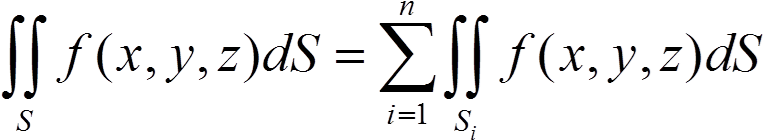Поверхностный интеграл первого рода. Основные определения и свойства

Пусть на поверхности S задана числовая функция f(x, y, z). На каждом участке поверхноcти S_i, выбираем по точке ξ_i и составляем интегральную сумму

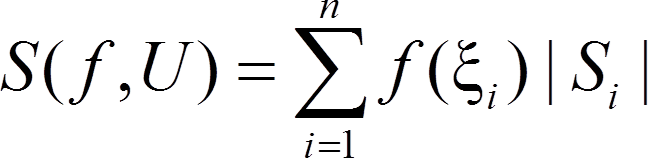
|S_i| — площадь участка поверхности S_i.

(1) 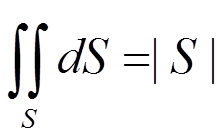 — (|S| — площадь поверхности S).

(2) 

(3) 

(4)

(5) Если U = {S₁, S₂, ..., S_n} — разбиение S, то