Условие независимости криволинейного интеграла от формы пути

Ω открытое множество в пространстве

(x, y) = {P(x, y, z), Q(x, y, z), R(x, y, z)}

(непрерывно дифференцируемое векторное поле в Ω)

(1) Для любой замкнутой кривой L в Ω

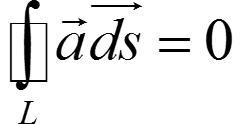
(2) Для любых кривых L₁ и L₂ с общими началами и концами

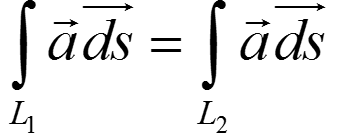
(3) Существует такая функция φ ∈ C¹(Ω), для которой

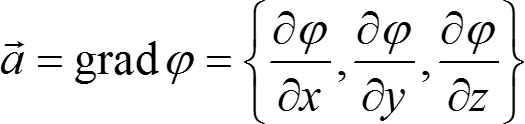
(4) Существует такая функция φ ∈ C¹(Ω), для которой

P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = dφ(x, y, z)

(5) Существует такая функция φ ∈ C¹(Ω), что для любых точек A, B ∈ Ω и любой кривой L с началом в точке A и концом в точке B