Понятие числового ряда и его сходимости

Пусть имеется числовая  последовательность u₁, u₂, ..., u_n, ... . Символ

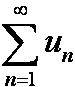u₁ + u₂ + ... + u_n + ... =    (1)

будем называть числовым рядом, а элементы последовательности — его членами. Общий член ряда u_n есть функция натурального аргумента. Рассмотрим теперь последовательность частичных сумм ряда (1):

S₁ = u₁,   S₂ = u₁ + u₂, ...,   S_n = u₁ + u₂ + ... + u_n, ... = .

Определение

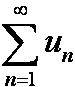Если существует конечный или нет предел последовательности частичных сумм S_n = S, то он называется суммой ряда (1), при этом пишут = S.

Если |S| < +∞, то ряд (1) называют сходящимся, если же  |S| = +∞, или не существует, то ряд называют расходящимся.