Несобственные интегралы
Следствие 11.2
Условие
1) f(z) аналитична в верхней полуплоскости Im z > 0, за исключением конечного числа изолированных особых точек ![]() .
.
2) zf(z) ![]() 0 при z → ∞, Im z > 0 равномерно относительно arg z.
0 при z → ∞, Im z > 0 равномерно относительно arg z.
Утверждение
Верны формулы
I = |
(11.5) |
Если f(x) — чётная функция, то
I = |
(11.6) |
Доказательство
Равенство (11.5) получается по той же схеме, по которой решался пример 11.3. А (11.6) следует из (11.5) и того факта, что интеграл по симметричному относительно нуля промежутку [−R, R] от чётной функции равен удвоенному интегралу от неё по правой половине [0, R] этого промежутка.


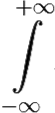 f(x)dx = 2πi
f(x)dx = 2πi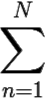 Res (f(an))
Res (f(an))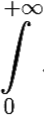 f(x)dx =
f(x)dx = 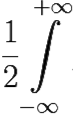 f(x)dx = πi
f(x)dx = πi
