Интегральная теорема Коши

Доказательство

1. Пусть контуры C₁ и C₂ не имеют общих точек, кроме начала и конца. Тогда они образуют один замкнутый контур
C = C₁ + C₂⁻, если мы начнём обход вдоль контура C₁ до его конца, а затем от конца контура C₂ к его началу. По теореме Коши 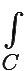f(z)dz = 0. Но по свойству аддитивности интеграла

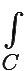f(z)dz = 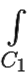f(z)dz + 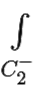f(z)dz = 0.

Таким образом, 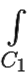f(z)dz = −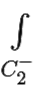f(z)dz.

Но по свойству интеграла −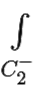f(z)dz = 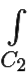f(z)dz, следовательно, 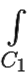f(z)dz = 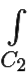f(z)dz.

2. Если же контуры C₁ и C₂ имеют общие точки, то контур C = C₁ + C₂⁻ есть объединение нескольких замкнутых контуров (и, возможно, нескольких участков, где они совпадают), для каждого из которых можно провести рассуждения доказательства пункта 1.