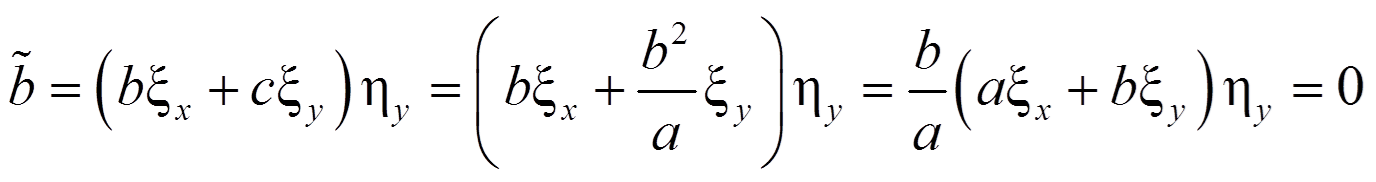Уравнения гиперболического, параболического и эллиптического типа

Уравнение параболического типа

b² − ac = 0

a = 0 ⇒ b = 0, с ≠ 0

⇔aφ_x + bφ_y = 0

Пусть ξ — решение характеристического уравнения

aξ_x + bξ_y = 0,

а η — любая функция, не зависящая от ξ. Тогда пара функций ξ, η даёт искомую замену переменных. Покажем это.

Так как функция ξ является решением характеристического уравнения, то

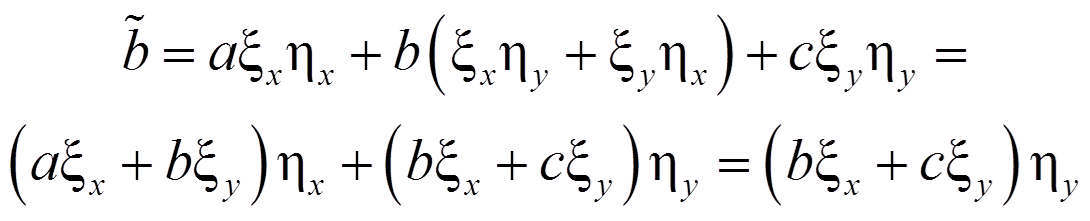
Из равенства нулю дискриминанта получаем