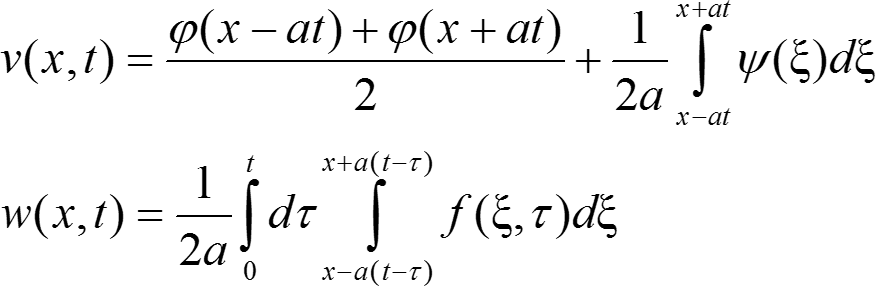Полная формула Даламбера. Теорема существования (достаточные условия разрешимости). Дифференцирование интеграла, зависящего от параметра
Теорема существования (достаточные условия разрешимости)
φ ∈ C2(R), ψ ∈ C1(R), f ∈ C1(x ∈ R, t ≥ 0)
В этом случае полная формула Даламбера даёт классическое и притом единственное решение задачи Коши.
u = ν + w |
|
Дифференцирование интеграла, зависящего от параметра
I(p) =  F(u, p)du
F(u, p)du
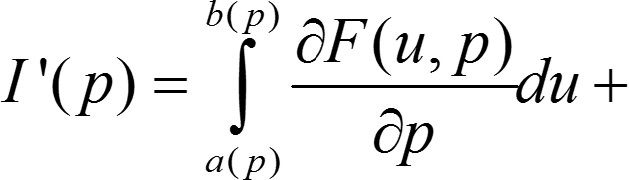
+ F(b(p), p)b′(p) − F(a(p), p)a′(p)