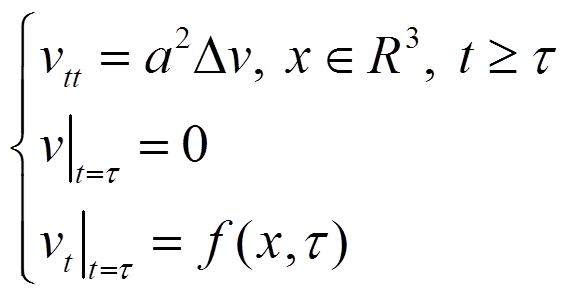Решение третьей задачи. Принцип Дюамеля. Полная формула Киргофа
u(x, t) = |
|
|
Δu = ut = |
utt = |
|
utt − a2Δu = |
|
u(x, t) = 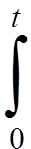 ν(x, t, τ)dτ, ut(x, t) =
ν(x, t, τ)dτ, ut(x, t) = 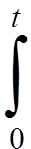 νt(x, t, τ)dτ
νt(x, t, τ)dτ
u(x, 0) = 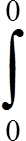 ν(x, 0, τ)dτ = 0, ut(x, 0) =
ν(x, 0, τ)dτ = 0, ut(x, 0) = 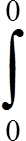 νt(x, 0, τ)dτ = 0
νt(x, 0, τ)dτ = 0


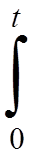 ν(x, t, τ)dτ =
ν(x, t, τ)dτ = 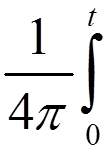 (t − τ)
(t − τ)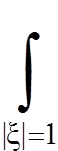 f(x + a(t − τ)ξ, τ)dSξdτ
f(x + a(t − τ)ξ, τ)dSξdτ