Распространение волн в пространстве. Принцип Гюйгенса

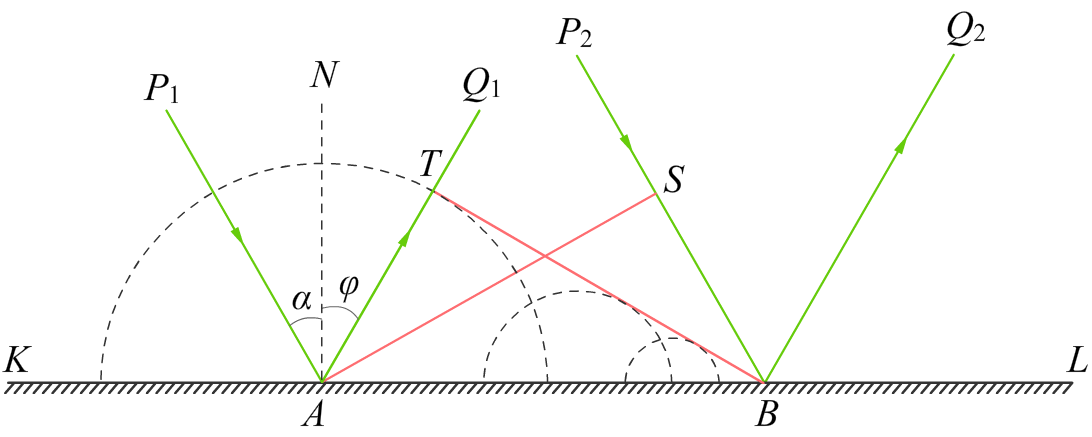
Все точки отрезка AB служат источниками вторичных волн. Раньше всего волновая поверхность AS приходит в точку A. Затем, по мере движения падающей волны, в колебательный процесс вовлекаются другие точки данного отрезка, и в самую последнюю очередь — точка B.

Сферическая волна с центром в A имеет на рис. 4 наибольший радиус. По мере приближения к точке B радиусы сферических вторичных волн, испущенных промежуточными точками, уменьшаются до нуля. Волновая поверхность BT отражённой волны есть плоскость, касательная ко всем этим Сферам. Теперь заметим, что радиус AT — это расстояние, пройденное вторичной волной с центром в A за то время, пока волновая поверхность AS двигается к точке B. Скажем это чуть по-другому: время движения вторичной волны от точки A до точки T равно времени движения падающей волны от точки S до точки B. Но скорости движения падающей и вторичной волн совпадают — ведь дело происходит в одной и той же среде! Поэтому, раз совпадают скорости и времена, то равны и расстояния: AT = BS. Получается, что прямоугольные треугольники ABT и ABS равны по гипотенузе и катету. Стало быть, равны и соответствующие острые углы: ∠ABT = ∠BAS. Остаётся заметить, что ∠ABT = φ (так как оба они равны 90° — ∠BAT ) и ∠BAS = α (оба они равны 90° — ∠NAS). Таким образом, φ = α — угол отражения равен углу падения.