Устранимая особенность
|
x ∈ Ω u(x) гармонична в Ω \ a (u(x) ∈ C2(Ω \ a), Δu(x) = 0 (x ∈ Ω \ a)) ∃ A =
|
Теорема о стирании особенности
Пусть u(x) гармонична в Ω \ a, причём при x → a
u(x) = o(E(x, a)),
тогда x = a является устранимой особой точкой.


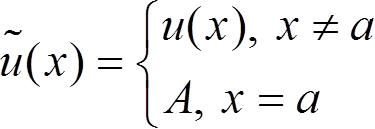 гармонична в
гармонична в 
