Национальный Исследовательский Ядерный
университет «МИФИ»
Кафедра Прикладной Математики
Лекции для Т8-31
университет «МИФИ»
Кафедра Прикладной Математики
Николай А. Кудряшов
Нелинейные Математические Модели
Лекции для Т8-31
Темы 1-ой лекции
1.1 Понятие о математической модели
1.2 Примеры математических моделей
1.3 Постановка математической задачи
1.4 Линейные и нелинейные математические модели
1.5 Приближение механики сплошной среды
1.6 Система уравнений газовой динамики
1.6.1 Уравнение непрерывности
1.6.2 Уравнение сохранения импульса
1.6.3 Уравнение сохранения энергии
1.2 Примеры математических моделей
1.3 Постановка математической задачи
1.4 Линейные и нелинейные математические модели
1.5 Приближение механики сплошной среды
1.6 Система уравнений газовой динамики
1.6.1 Уравнение непрерывности
1.6.2 Уравнение сохранения импульса
1.6.3 Уравнение сохранения энергии
1.1а Понятие о математической модели
- В переводе с латинского модель — это мера, образ, способ.
- Описание физического процесса достоверно, если его можно выразить с помощью числовой величины
- Чтобы определить величины часто приходится решать математические задачи
- Математическая модель — это задача сформулированаая языком математики.
1.1б Понятие о математической модели
- Математическая модель — это задача, соответствующая реальному описанию процесса.
- Главное требование математической модели — адекватное описание процесса.
- Это достигается прежде всего использованием законов сохраения при описании модели
- Сравнением характеристик полученных при расчетах и при эксперименте
Пример математической модели

Пример математической модели
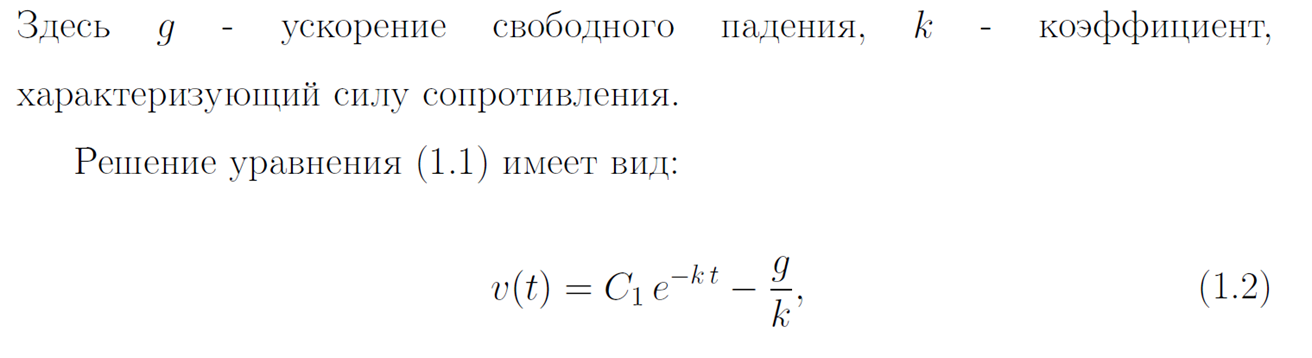
Пример математической модели


Постановка математических задач

Постановка задач (2)

Линейные и нелинейные модели

Линейные и нелинейные модели (2)

Линейные и нелинейные модели (3)

Приближение механики сплошной среды

Система уравнений газовой динамики (1)


Система уравнений газовой динамики (2)

Система уравнений газовой динамики (3)

Система уравнений газовой динамики (4)

Система уравнений газовой динамики (5)

Система уравнений газовой динамики (6)
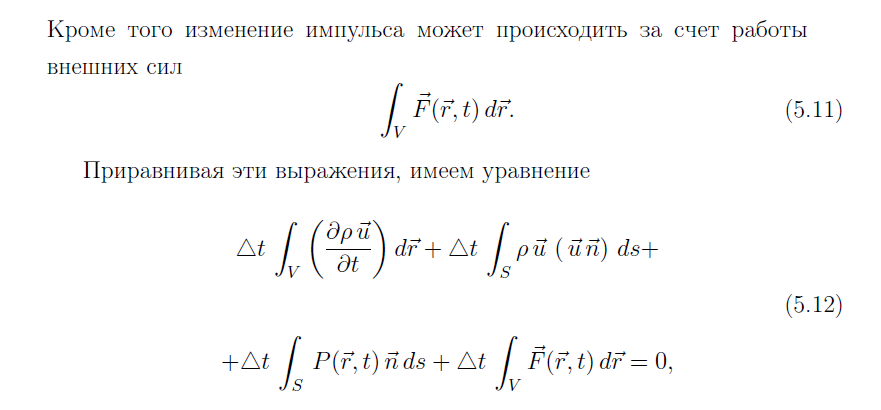
Система уравнений газовой динамики (7)
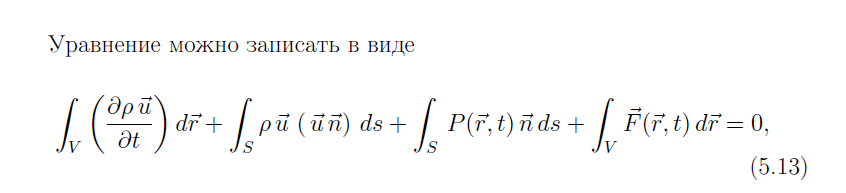

Система уравнений газовой динамики (8)
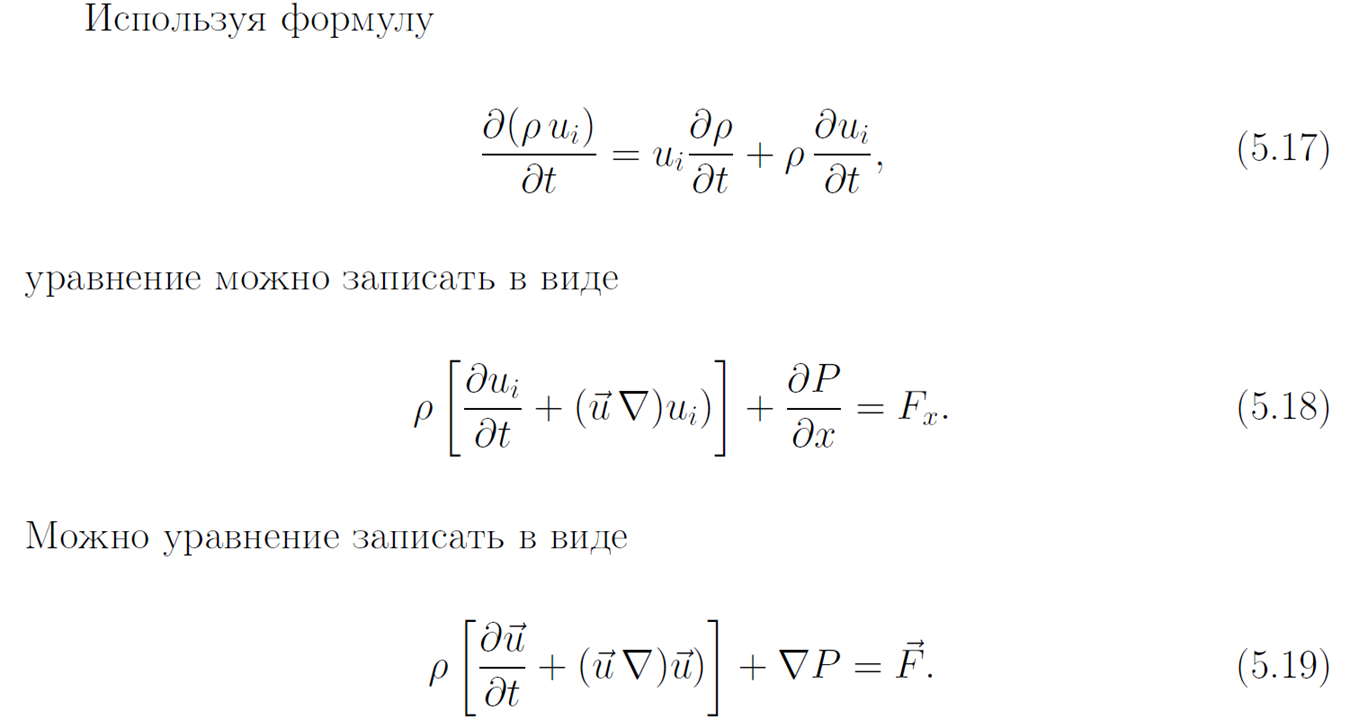
Система уравнений газовой динамики (9)

Система уравнений газовой динамики (10)
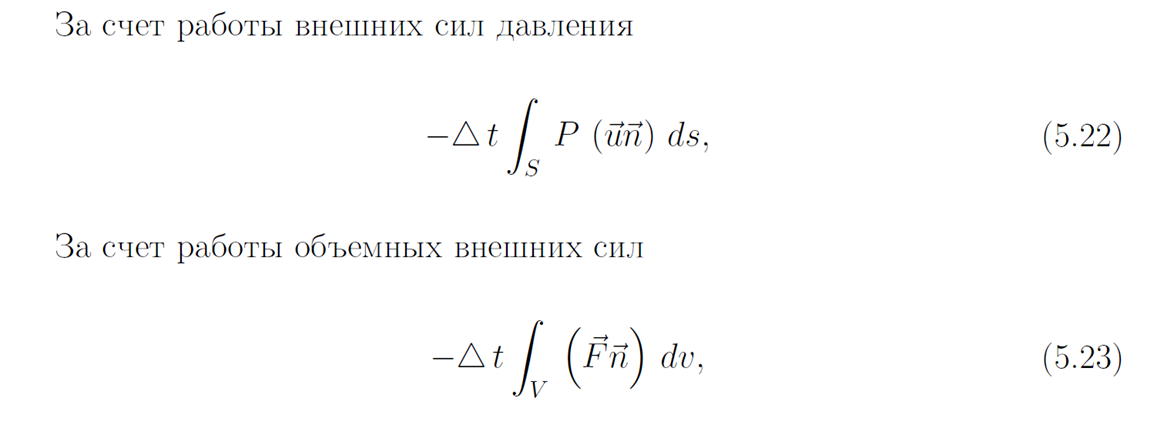
Система уравнений газовой динамики (10)
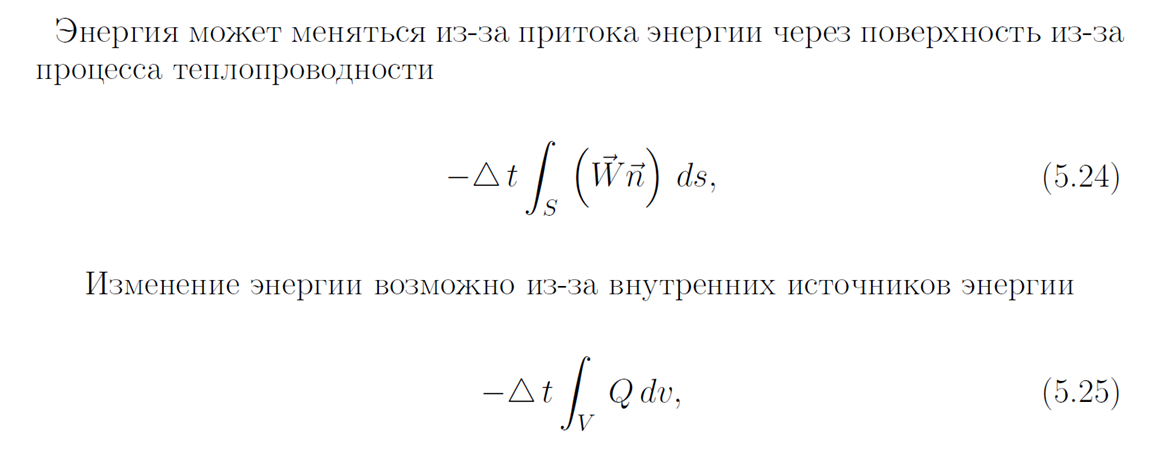
Система уравнений газовой динамики (10)

Система уравнений газовой динамики (11)
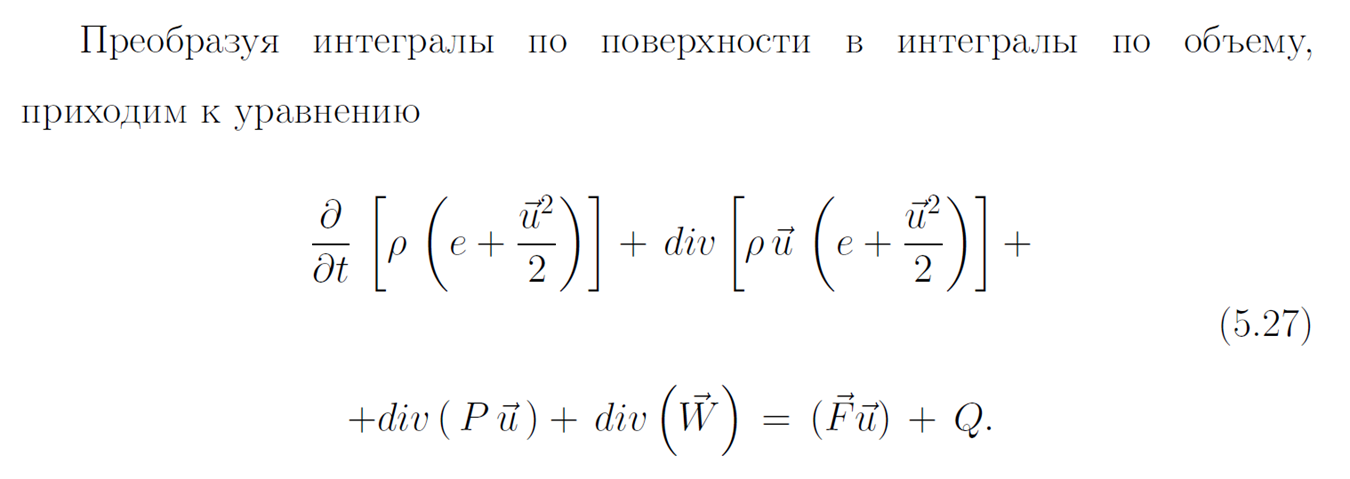
Система уравнений газовой динамики

Постановка задач для газовой динамики

Постановка задач для системы уравнений газовой динамики

