Измерительная информация и её количественные характеристики

Измерение — это по­лу­че­ние ин­фор­ма­ции. С точ­ки зре­ния тео­рии ин­фор­ма­ции, ос­но­вы ко­то­рой за­ло­же­ны аме­ри­кан­ским учё­ным Кло­дом Шен­но­ном, из­ме­ря­е­мая ве­ли­чи­на до вы­пол­не­ния из­ме­ре­ний об­ла­да­ет не­опре­де­лён­но­стью, ко­то­рая ха­рак­те­ри­зу­ет­ся зна­че­ни­ем без­услов­ной эн­тро­пии

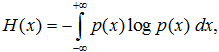
где p(x) — плот­ность рас­пре­де­ле­ния ве­ро­ят­но­стей воз­мож­ных зна­че­ний из­ме­ря­е­мой ве­ли­чи­ны x. Эн­тро­пию H(x) мож­но трак­то­вать как сред­нюю не­опре­де­лён­ность ис­точ­ни­ка ин­фор­ма­ции до на­ча­ла про­цес­са из­ме­ре­ний.

Ко­ли­че­ство ин­фор­ма­ции I, по­лу­ча­е­мое в ре­зуль­та­те из­ме­ре­ния, рав­но убы­ли не­опре­де­лён­но­сти, то есть раз­но­сти эн­тро­пий до и по­сле из­ме­ре­ния:

Здесь I — без­услов­ная (апри­ор­ная) эн­тро­пия, опи­сы­ва­е­мая плот­но­стью ве­ро­ят­но­стей p(x) из­ме­ря­е­мой ве­ли­чи­ны x до на­ча­ла про­цес­са из­ме­ре­ний. H(x/x_u) — услов­ная эн­тро­пия, т. е. эн­тро­пия ве­ли­чи­ны x при усло­вии, что по­лу­чен ре­зуль­тат из­ме­ре­ний x_u. Услов­ная эн­тро­пия — ме­ра остав­шей­ся не­опре­де­лён­но­сти из­ме­ря­е­мой ве­ли­чи­ны x по­сле по­лу­че­ния от­счё­та x_u, вы­зван­ная на­ли­чи­ем по­греш­но­стей, по­мех и соб­ствен­ных шу­мов в из­ме­ри­тель­ной си­сте­ме. Ес­ли бы в из­ме­ри­тель­ной си­сте­ме от­сут­ство­ва­ли соб­ствен­ные шу­мы и по­греш­но­сти из­ме­ре­ний, то ко­ли­че­ство по­лу­ча­е­мой в экс­пе­ри­мен­те ин­фор­ма­ции рав­ня­лось бы без­услов­ной эн­тро­пии, т. е. не­опре­де­лён­ность при из­ме­ре­ни­ях сни­ма­лась бы пол­но­стью и услов­ная эн­тро­пия рав­ня­лась бы ну­лю. Оче­вид­но, что в ре­аль­ных из­ме­ри­тель­ных си­сте­мах это не­воз­мож­но. По­это­му по­те­ри ин­фор­ма­ции от по­мех, шу­ма и слу­чай­ных по­греш­но­стей из­ме­ре­ний рав­ны эн­тро­пии по­мех, шу­ма и слу­чай­ных по­греш­но­стей.

Ес­ли из­ме­ри­тель­ный при­бор име­ет диа­па­зон из­ме­ре­ний от X₁ до X₂, в пре­де­лах ко­то­ро­го ожи­да­ет­ся по­лу­че­ние из­ме­ря­е­мо­го зна­че­ния x_u, то без­услов­ная эн­тро­пия H(x) ис­точ­ни­ка ин­фор­ма­ции, при усло­вии рав­но­мер­но­го за­ко­на рас­пре­де­ле­ния ве­ро­ят­но­сти по­лу­чить от­счёт на шка­ле при­бо­ра бу­дет рав­на:

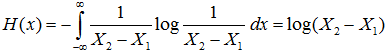
Услов­ная эн­тро­пия опре­де­ля­ет­ся за­ко­ном рас­пре­де­ле­ния по­греш­но­сти Δ из­ме­ри­тель­но­го устрой­ства и рав­на:

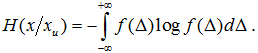
Ес­ли по­греш­ность рав­но­мер­но рас­пре­де­ле­на на ин­тер­ва­ле то услов­ная эн­тро­пия рав­на:

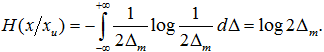
При нор­маль­ном рас­пре­де­ле­нии по­греш­но­сти с дис­пер­си­ей σ ² услов­ная эн­тро­пия рав­на:

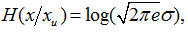
где e — ос­но­ва­ние на­ту­раль­ных ло­га­риф­мов; σ — сред­не­квад­ра­ти­че­ское от­кло­не­ние по­греш­но­сти. Срав­не­ние (1.4) и (1.5) по­ка­зы­ва­ет, что сред­ства из­ме­ре­ний, име­ю­щие су­ще­ствен­но раз­лич­ные за­ко­ны рас­пре­де­ле­ния по­греш­но­стей, мо­гут да­вать оди­на­ко­вое ко­ли­че­ство ин­фор­ма­ции при из­ме­ре­нии. В дан­ном слу­чае это бу­дет обес­пе­че­но при вы­пол­не­нии усло­вия В свя­зи с этим в ка­че­стве ха­рак­те­ри­сти­ки дез­ин­фор­ма­ци­он­но­го дей­ствия по­греш­но­сти с про­из­воль­ным за­ко­ном рас­пре­де­ле­ния мож­но ис­поль­зо­вать эн­тро­пий­ное зна­че­ние по­греш­но­сти.

Эн­тро­пий­ным зна­че­ни­ем по­греш­но­сти счи­та­ет­ся наи­боль­шее зна­че­ние по­греш­но­сти с рав­но­мер­ным за­ко­ном рас­пре­де­ле­ния, ко­то­рое вно­сит та­кую же дез­ин­фор­ма­цию, как и по­греш­ность с дан­ным за­ко­ном рас­пре­де­ле­ния ве­ро­ят­но­стей.

Ес­ли по­греш­ность опи­сы­ва­ет­ся нор­маль­ным за­ко­ном рас­пре­де­ле­ния, то эн­тро­пий­ное зна­че­ние по­греш­но­сти рав­но:

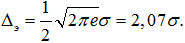
Ана­ло­гич­но опре­де­ля­ет­ся эн­тро­пий­ное зна­че­ние по­греш­но­сти для лю­бо­го кон­крет­но­го за­ко­на рас­пре­де­ле­ния. За­ви­си­мость меж­ду эн­тро­пий­ным и сред­не­квад­ра­ти­че­ским зна­че­ни­я­ми по­греш­но­сти мо­жет быть пред­став­ле­на в ви­де:

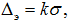
где k — эн­тро­пий­ный ко­эф­фи­ци­ент.

Эн­тро­пий­ный ко­эф­фи­ци­ент опре­де­ля­ет­ся ви­дом за­ко­на рас­пре­де­ле­ния ве­ро­ят­но­стей по­греш­но­стей. Для нор­маль­но­го (гаус­сов­ско­го) рас­пре­де­ле­ния эн­тро­пий­ный ко­эф­фи­ци­ент в со­от­вет­ствии с фор­му­лой (1.6) ра­вен

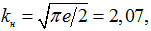
а для рав­но­мер­но­го рас­пре­де­ле­ния

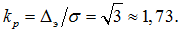
По­лу­чен­ные зна­че­ния эн­тро­пий­но­го ко­эф­фи­ци­ен­та ха­рак­те­ри­зу­ют об­ласть его зна­че­ний, со­от­вет­ству­ю­щую боль­шин­ству ре­аль­ных за­ко­нов рас­пре­де­ле­ния ве­ро­ят­но­стей по­греш­но­сти. Ана­лиз зна­че­ний эн­тро­пий­но­го ко­эф­фи­ци­ен­та поз­во­ля­ет сде­лать вы­вод, что при оди­на­ко­вом сред­не­квад­ра­ти­че­ском зна­че­нии по­греш­ность, рас­пре­де­лён­ная по нор­маль­но­му за­ко­ну, вно­сит боль­шую дез­ин­фор­ма­цию, чем по­греш­ность, рас­пре­де­лён­ная по рав­но­мер­но­му за­ко­ну. Бо­лее то­го, дез­ин­фор­ма­ци­он­ное дей­ствие по­греш­но­сти с лю­бым дру­гим за­ко­ном рас­пре­де­ле­ния мень­ше дез­ин­фор­ма­ци­он­но­го дей­ствия по­греш­но­сти с нор­маль­ным за­ко­ном рас­пре­де­ле­ния при их оди­на­ко­вых сред­не­квад­ра­ти­че­ских зна­че­ни­ях.

Ин­фор­ма­ци­он­ный под­ход да­ёт воз­мож­ность с еди­ных по­зи­ций ана­ли­зи­ро­вать лю­бые сред­ства из­ме­ре­ний (из­ме­ри­тель­ные пре­об­ра­зо­ва­те­ли, из­ме­ри­тель­ные при­бо­ры, из­ме­ри­тель­ные ин­фор­ма­ци­он­ные си­сте­мы) как в ста­ти­че­ском, так и в ди­на­ми­че­ском ре­жи­мах ра­бо­ты, вы­яв­лять вза­и­мо­свя­зи раз­лич­ных тех­ни­че­ских ха­рак­те­ри­стик средств из­ме­ре­ний, оп­ти­ми­зи­ро­вать эти ха­рак­те­ри­сти­ки и оце­ни­вать пре­дель­ные воз­мож­но­сти ис­поль­зу­е­мых средств из­ме­ре­ний.