Статические характеристики средств измерений
1. Функция (характеристика) преобразования — функциональная зависимость выходной величины y от входной x, которая может быть задана формулой, таблицей, графиком. В аналитическую функцию преобразования y = f(x) обычно входят конструктивные параметры прибора или функционального преобразователя, используемые при их расчёте или проектировании. Функция преобразования реального преобразователя определяется экспериментально. Желательно, чтобы функция преобразования была линейной:
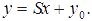
2. Чувствительность преобразования S — отношение изменения выходной величины прибора или измерительного преобразователя к вызвавшему её изменению входной величины
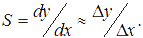
Чувствительность может быть определена при любом способе задания функции преобразования. В частном случае линейного преобразования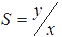 
, где y — значение выходной величины, соответствующей входной x. Возможно задание относительной чувствительности преобразования 
.
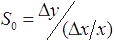3. Порог чувствительности Δx — изменение значения измеряемой величины, способное вызвать наименьшее обнаруживаемое изменение выходной величины. Порог чувствительности препятствует обнаружению сколь угодно малых сигналов. Это обусловлено наличием в любой физической системе случайных флуктуаций (шум), затрудняющих выявление сигнала на фоне шума. Шум в измерительной системе может быть вызван многими причинами, такими как тепловые флуктуации (шум резистора), квантовый характер потока носителей зарядов (дробовой шум в полупроводниках) и т. д. Существуют и другие источники возмущений, например, механические дефекты (трение, люфт), механические вибрации, электрические наводки, ухудшающие порог чувствительности. Однако эти факторы могут быть устранены, часто простым изменением конструкции измерительной системы. Теоретически достижимый порог чувствительности (предельный порог чувствительности) определяется собственными шумами системы и может быть определён как наименьший входной сигнал, который можно обнаружить с определённой степенью достоверности на фоне собственного шума измерительной системы. Например, при условии, что отношение «сигнал/шум» на выходе этой системы равно единице.
4. Статические погрешности средств измерений. Каждое измерение сопровождается погрешностью. Различают систематические и случайные, абсолютные и относительные, основные и дополнительные погрешности измерений, источники и причины которых будут системно проанализированы в курсе метрологии измерений. Здесь же рассмотрим погрешности, вызванные отклонением функции преобразования измерительной системы от номинальной характеристики, описываемой соотношением (2.1). Погрешность, обусловленная изменением значений y0 при нулевом значении входной величины x, называется аддитивной погрешностью, или погрешностью нуля преобразования. Погрешность, вызванная отклонением значения S от номинального, называется мультипликативной, или погрешностью чувствительности преобразования. Аддитивная погрешность не зависит от значения входной величины, а мультипликативная погрешность пропорциональна входной величине.
5. Статическая нелинейность. В измерительной системе с независящей от частоты чувствительностью (статические системы) соотношение между выходным сигналом и входным, как правило, линейно. Реальная измерительная система не является идеально линейной, она всегда линейна лишь приближённо (например, в малом интервале значений входного сигнала). Причинами отклонений от линейности являются: гистерезис, мёртвая зона, насыщение. Степень статической (частотно-независимой) нелинейности определяется соотношением:
f(x) — реальная зависимость между y и x, а y = ax — линейное приближение f(x).
6. Помимо перечисленных, статическими характеристиками измерительных систем являются: пределы измерений — наибольшее и наименьшее значения измеряемой величины, для которых нормированы погрешности; диапазон измерений — область значений, заключённая между верхним и нижним пределами измерений; надёжность — способность сохранять заданные характеристики средства измерения в течение заданного времени.
