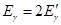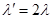Пусть  обозначает длину волны налетающего фотона, а
обозначает длину волны налетающего фотона, а  — длину волны рассеянного фотона. Из рисунка 1 видно, что углом рассеяния называется угол между векторами импульсов налетающего и рассеянного фотонов. Изменение длины волны в результате комптоновского рассеяния на электроне связано с углом рассеяния фотона
— длину волны рассеянного фотона. Из рисунка 1 видно, что углом рассеяния называется угол между векторами импульсов налетающего и рассеянного фотонов. Изменение длины волны в результате комптоновского рассеяния на электроне связано с углом рассеяния фотона  соотношением
соотношением

|
(1) |
где  — комптоновская длина волны электрона:
— комптоновская длина волны электрона:

|
(2) |
Здесь me масса электрона, а c — скорость света в вакууме.
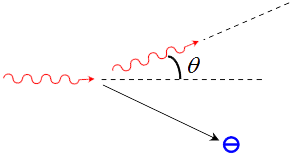
Рисунок 1
Энергия налетающего фотона связана с его частотой 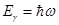 , причём частота
, причём частота 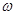 может быть выражена через длину волны:
может быть выражена через длину волны:  . Тогда энергии налетающего и рассеянного фотонов запишутся так:
. Тогда энергии налетающего и рассеянного фотонов запишутся так:

|
(3) |
Энергия покоящегося свободного электрона равна mec2. После столкновения с фотоном электрон приобретает кинетическую энергию 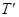 , так, что его полная энергия становится равной
, так, что его полная энергия становится равной 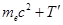 . Закон сохранения энергии для комптоновского рассеяния выглядит следующим образом:
. Закон сохранения энергии для комптоновского рассеяния выглядит следующим образом:
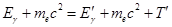
|
(4) |
По условию задачи энергия рассеянного фотона равна кинетической энергии электрона отдачи, т. е. 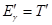 . Подставляя это соотношение в (4), и сокращая на
. Подставляя это соотношение в (4), и сокращая на 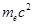 , получаем:
, получаем:
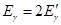
|
(5) |
Теперь, используя формулы (3) и уравнение (5), получаем следующую связь:
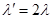
|
(6) |
 обозначает длину волны налетающего фотона, а
обозначает длину волны налетающего фотона, а  — длину волны рассеянного фотона. Из рисунка 1 видно, что углом рассеяния называется угол между векторами импульсов налетающего и рассеянного фотонов. Изменение длины волны в результате комптоновского рассеяния на электроне связано с углом рассеяния фотона
— длину волны рассеянного фотона. Из рисунка 1 видно, что углом рассеяния называется угол между векторами импульсов налетающего и рассеянного фотонов. Изменение длины волны в результате комптоновского рассеяния на электроне связано с углом рассеяния фотона  соотношением
соотношением
 — комптоновская длина волны электрона:
— комптоновская длина волны электрона:

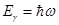 , причём частота
, причём частота 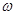 может быть выражена через длину волны:
может быть выражена через длину волны:  . Тогда энергии налетающего и рассеянного фотонов запишутся так:
. Тогда энергии налетающего и рассеянного фотонов запишутся так:
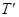 , так, что его полная энергия становится равной
, так, что его полная энергия становится равной 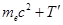 . Закон сохранения энергии для комптоновского рассеяния выглядит следующим образом:
. Закон сохранения энергии для комптоновского рассеяния выглядит следующим образом: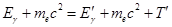
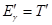 . Подставляя это соотношение в (4), и сокращая на
. Подставляя это соотношение в (4), и сокращая на 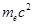 , получаем:
, получаем: