Согласно волновым представлениям о движении микрочастиц, электронам может быть приписана длина волны де Бройля, связанная с их импульсом , следующим соотношением:

Пучок электронов с длиной волны испытывает дифракцию на монокристалле, которая описывается таким же способом как дифракция рентгеновского излучения на монокристалле. В приближении Брэгга — Вульфа дифракцию излучения на кристалле можно интерпретировать как результат интерференции двух пучков, зеркально отражённых от соседних атомных плоскостей (рисунок 1).

Рисунок 1

Условие дифракционного максимума для отражённых пучков определяется формулой Брэгга — Вульфа:

где — межплоскостное расстояние, 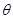— угол скольжения, показанный на рисунке, а — целое число, определяющее порядок дифракционного максимума.

Определим импульс электронов, падающих на монокристалл. Электроны, прошедшие ускоряющую разность потенциалов , приобретают дополнительную энергию , где — элементарный заряд. Учитывая, что начальная скорость электронов равна нулю, запишем закон сохранения энергии электрона

где и — импульс и масса электрона. Заметим, что здесь использована нерелятивистская формула для кинетической энергии, поскольку в подобных задачах энергия всегда меньше энергии покоя электрона.

Из формулы (2) находим импульс электронов