, следующим соотношением: Согласно волновым представлениям о движении микрочастиц, электронам может быть приписана длина волны де Бройля, связанная с их импульсом , следующим соотношением:
|
(1) |
Движение микрочастицы с таким импульсом и длиной волны ограничено областью потенциальной ямы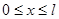 
. Вне этой области микрочастица находиться не может, поскольку её энергия была бы бесконечной.
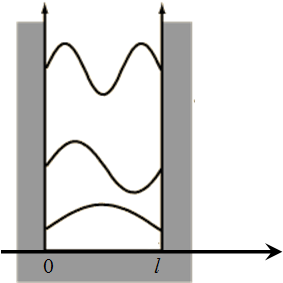
Рисунок 1
Известно, что при распространении волн в замкнутой области возникает система стоячих волн. Волновой процесс, который связывается с движением микрочастицы в потенциальной яме, также приобретает форму стоячих волн. Пси-функция, определяющая вероятность местонахождения микрочастицы, должна обращаться в нуль на границах потенциальной ямы пр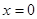и 
и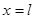 
. Следовательно, на границах ямы находятся узлы стоячей волны, причём на длине 
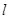должно укладываться целое число полуволн де Бройля, т. е.
|
(2) |
Общая картина процесса, аналогичная стоячим волнам на струне с закреплёнными концами, схематически изображена на рисунке 1. В нижней части рисунка показана первая гармоника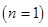 
, когда на длине 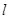укладывается половина длины волны. В средней и верхней части рисунка 1 показаны формы стоячей волны для второй и третьей гармоник.
Подставляя длину волны де Бройля (1) в формулу (2), получаем:
|
(3) |
