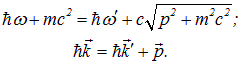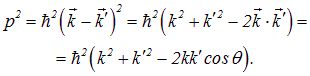2.4. Эффект Комптона

Наиболее ярко и полно корпускулярные свойства света проявляются в эффекте Комптона. Американский физик А. Комптон, исследуя рассеяние монохроматических рентгеновских лучей веществами с не очень большими атомными номерами (например, бором или графитом), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также излучение более длинных волн . С точки зрения волновой оптики это выглядело так же странно, как если бы человек в синем свитере, посмотрев в зеркало, увидел себя одетым в красное. Но именно в подобном «покраснении» суть наблюдавшегося эффекта, который получил простое объяснение в рамках концепции фотонов: из-за закона сохранения часть фотонного импульса передается электрону, энергия фотона уменьшается и, следовательно, уменьшается его частота, то есть фотон «краснеет».

 

Рис. 2.18. А́ртур Хо́лли Ко́мптон (1892–1962)

Опыты показали, что разность

не зависит от длины волны  падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния  между направлениями рассеянного излучения и первичного пучка:

где  — длина волны рассеянного излучения, m —  масса покоя электрона,  —  постоянная Планка, с — скорость света в вакууме.

В легких веществах, с которыми производились опыты Комптона, энергия связи электрона с атомом и кинетическая энергия движения электронов вокруг ядра малы по сравнению с энергией, передаваемой ему рентгеновским квантом при столкновении, то есть в легких атомах энергией связи электрона внутри атома можно пренебречь и считать все электроны свободными и покоящимися.

Рассмотрим столкновение фотона со свободным покоящимся электроном, применяя законы сохранения энергии и импульса как при соударении упругих шаров (рис. 2.19).

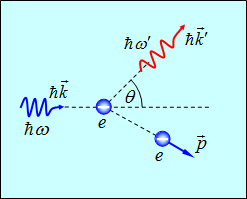
Рис. 2.19. Эффект Комптона как упругое столкновение фотона с электроном

Видео 2.3. Эффект Комптона и фотопоглощение — основные процессы в веществе сцинтиллятора ФЭУ

Фотон с энергией  и импульсом   падает на первоначально покоящийся свободный электрон . Энергия электрона до столкновения равна  ( — масса электрона). После столкновения электрон в результате отдачи будет обладать импульсом p и энергией

Энергия и импульс фотона после рассеяния изменятся и станут равными   и  . Запишем законы сохранения энергии и импульса:

Учитывая, что , перепишем закон сохранения энергии в виде

или

Уравнение закона сохранения импульса после возведения в квадрат дает

Приравнивая правые части полученных соотношений (2.13) и (2.14), находим

После деления (2.15) на произведение  и умножения его на  получаем

Длина волны фотона связана с волновым числом соотношением , поэтому

где величина

называется комптоновской длиной волны частицы с массой m (в данном случае — электрона). Величину

также называют комптоновской длиной волны электрона, так что мы будем различать их обозначения:  и  .

Эксперименты показывают, что в составе рассеянного излучения присутствует несмещенная линия (излучение с первоначальной длиной волны), что можно объяснить следующим образом. Величина смещения , как мы убедились, когда рассмотрели рассеяние фотона на свободном электроне, обратно пропорциональна его массе. Однако фотон может обмениваться энергией и импульсом с атомом в целом. Так как масса атома велика по сравнению с массой электрона, то атому передается ничтожно малая доля энергии фотона. Поэтому в этом случае длина волны  рассеянного излучения практически не будет отличаться от длины волны  падающего излучения.