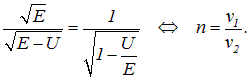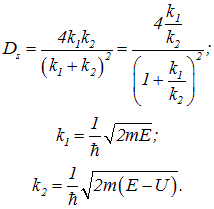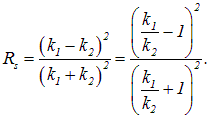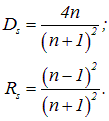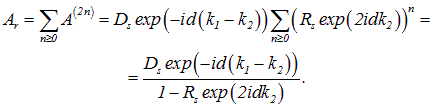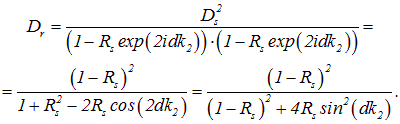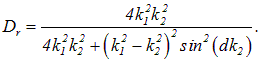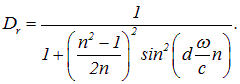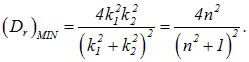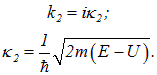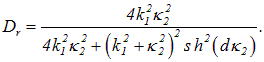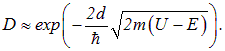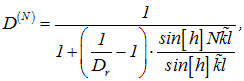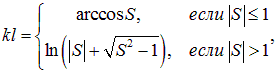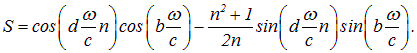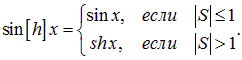4.8. Оптическая аналогия прохождения частицы над барьером
В этом разделе мы покажем, что прохождение квантовой частицы через низкий потенциальный барьер аналогично отражению света на границе двух полубесконечных сред. Далее, прохождение частицы через потенциальный барьер конечной ширины может быть описано как множественное отражение классических волн, и в результате опять-таки мы придем к известным результатам оптики. Целью данного раздела является демонстрация тесной связи различных областей физики.
Ступенчатый потенциал
Этот потенциал мы снова изобразим на рис. 4.19.
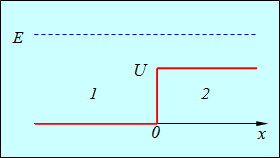
Рис. 4.19. Прохождение частицы над ступенчатым барьером:
процесс эквивалентен нормальному падению света из вакуума (1)
на полубесконечную среду (2) с показателем преломления

Установление аналогии между квантовой механикой и светом означает, что мы хотим найти такие замены квантово-механических характеристик движения частицы на характеристики света, чтобы формулы квантовой механики перешли в соответствующие формулы для распространения света. Процедура замены будет изображена в формулах двойными стрелками, причем слева будут стоять квантово-механические величины, а справа — оптические. От этих формул следует отличать равенства, где по обе стороны стоят величины, относящиеся либо к частице, либо к световой волне.
Распространение квантовой частицы описывается в терминах ее волнового вектора
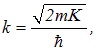
где
![]()
— кинетическая энергия частицы. Здесь и далее мы выписываем для частицы формулы, относящиеся к области барьера; соотношения для частицы вне барьера получаются при 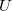 = 0. Скорость частицы дается соотношением
= 0. Скорость частицы дается соотношением
|
|
|
(4.36) |
Введем прежде всего показатель преломления 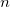 среды 2, соответствующий области барьера: его естественно определить, как отношение скоростей частицы в областях 1 и 2 (считаем, что в области 1 показатель преломления равен единице, как в вакууме, то есть
среды 2, соответствующий области барьера: его естественно определить, как отношение скоростей частицы в областях 1 и 2 (считаем, что в области 1 показатель преломления равен единице, как в вакууме, то есть ![]() )
)
|
|
|
(4.37) |
При 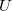 = 0 получаем n = 1 — показатель преломления вакуума.
= 0 получаем n = 1 — показатель преломления вакуума.
Волновой вектор световой волны связан с круговой частотой соотношением
![]()
Мы предположим также, что волновой вектор частицы перейдет при искомой замене в волновой вектор света, то есть
|
|
|
(4.38) |
Из соотношения
![]()
для среды без дисперсии следует групповая скорость света
![]()
в которую при искомой замене должна перейти скорость частицы  . Тогда уравнение (4.36) дает
. Тогда уравнение (4.36) дает
|
|
|
(4.39) |
Разделив уравнение (4.38) на (4.39), находим еще одну замену
|
|
|
(4.40) |
Конечно, «массу», стоящую здесь в левой части, нельзя отождествлять с массой фотона, которая равна нулю. Можно назвать ее «эффективной массой фотона». В вакууме, при n = 1, она равна
![]()
Эта величина соответствует известной релятивистской связи масса — энергия, и она возникает при изучении влияния гравитационного поля на распространение света.
Как бы то ни было, но суть в том, что указанные замены, как мы увидим, переводят формулы квантовой механики в формулы оптики.
Рассматривая прохождение частицы над низким потенциальным барьером (см. ступенчатый потенциал на рис. 4.19), мы уже вывели коэффициент прохождения, который здесь обозначим ![]() :
:
|
|
|
(4.41) |
Коэффициент отражения (30.32), равный ![]() , переписываем в виде
, переписываем в виде
|
|
|
(4.42) |
Применяя вышеуказанные замены, сводящиеся в данном случае к замене
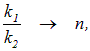
мы записываем соответствующие коэффициенты прохождения и отражения для света, падающего перпендикулярно из вакуума на среду с показателем преломления 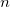 :
:
|
|
|
(4.43) |
В оптике точно такие формулы называются формулами Френеля для относительной интенсивности отраженного и преломленного света при угле падения 90°. Мы еще раз убедились, что физика (или природа) — едина, и квантовая механика имеет глубокие корни не только в классической механике, но и в волновой оптике.

Рис. 4.20. Огюсте́н Жан Френе́ль (1788 –1827)
Прямоугольный барьер конечной ширины
Потенциальный барьер показан на рис. 4.21.
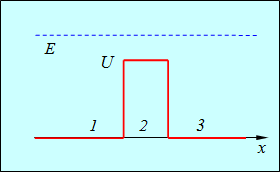
Рис. 4.21. Прохождение частицы над конечным прямоугольным барьером:
процесс эквивалентен многократным отражениям от барьера, показанного на рис. 4.19
Решение задачи можно выполнить стандартным образом, записывая суперпозицию плоских волн для каждой из трех областей 1, 2 и 3 и сшивая затем решения, чтобы найти амплитуды волн. Однако мы заменим такой рутинный способ на классическое рассмотрение прохождения волн, что позволит выявить физический смысл получающегося результата.
Заметим прежде всего, что конечный барьер можно рассматривать как наложение двух ступенчатых барьеров, расположенных в точках 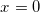 и
и 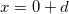 . Это замечание дает возможность использовать ранее полученные формулы.
. Это замечание дает возможность использовать ранее полученные формулы.
Пусть волна де Бройля с амплитудой, равной единице, движется слева направо и проникает в область над барьером в точке 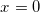 . Вследствие частичного отражения ее амплитуда уменьшается и становится равной
. Вследствие частичного отражения ее амплитуда уменьшается и становится равной
![]()
где ![]() — коэффициент прозрачности ступенчатого барьера. Далее она распространяется до точки
— коэффициент прозрачности ступенчатого барьера. Далее она распространяется до точки 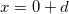 , приобретая на пути сдвиг фазы
, приобретая на пути сдвиг фазы
![]()
по сравнению с фазой свободной частицы в этой же точке. Здесь волна снова встречается со ступенчатым барьером, в результате чего ее амплитуда вновь уменьшается до величины
![]()
В результате волна выйдет за барьер с амплитудой
|
|
|
(4.44) |
Но мы учли только часть волны, выходящей наружу. Пришедшая в точку 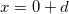 волна частично отражается от нее (дополнительный множитель
волна частично отражается от нее (дополнительный множитель
![]()
в амплитуде), идет назад в точку 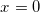 , снова отражается там (множитель
, снова отражается там (множитель
![]()
в амплитуде), возвращается назад в точку 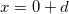 , где и выходит наружу. Полный пройденный этой частью волны путь равен 3d, дает сдвиг фазы
, где и выходит наружу. Полный пройденный этой частью волны путь равен 3d, дает сдвиг фазы
![]()
В результате эта часть волны выйдет за барьер с амплитудой
|
|
|
(4.45) |
Аналогичным образом происходят процессы с 2n отражениями внутри барьера, и каждый из них приводит к волне с амплитудой
|
|
|
(4.46) |
Амплитуда ![]() результирующей волны получается суммированием выражения (4.46) по всем n от нуля до бесконечности:
результирующей волны получается суммированием выражения (4.46) по всем n от нуля до бесконечности:
|
|
|
(4.47) |
Модуль амплитуды ![]() прошедшей над барьером волны даст нам коэффициент прохождения
прошедшей над барьером волны даст нам коэффициент прохождения ![]()
|
|
|
(4.48) |
Подставляя сюда квантово-механическое выражение (4.42) для ![]() , получаем
, получаем
|
|
|
(4.49) |
Стандартное решение уравнения Шредингера дает в точности такой же результат. Переходя к оптике, заменяем ![]() на выражение (4.43) и
на выражение (4.43) и ![]() — на
— на ![]() . Получаем тогда коэффициент прозрачности пластины конечной толщины
. Получаем тогда коэффициент прозрачности пластины конечной толщины 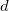 при нормальном падении света с частотой
при нормальном падении света с частотой ![]() :
:
|
|
|
(4.50) |
Это выражение также в точности воспроизводит результат волновой оптики.
Подобным образом можно рассмотреть отраженную от барьера волну, но результат нам уже известен: коэффициент отражения от конечного барьера можно вычислить по формуле
![]()
Изучая формулы (4.49) и (4.50), мы обнаруживаем «окна прозрачности» при некоторых значениях частоты падающего света, когда ![]() то есть нет никакой отраженной волны. Это случается при
то есть нет никакой отраженной волны. Это случается при
![]()
то есть когда четное число полуволн (или целое число волн) света в среде укладывается в двойной ширине барьера:
![]()
В обратном случае, когда двойная ширина барьера равна нечетному числу полуволн
![]()
мы приходим к минимальному значению коэффициента прозрачности
|
|
|
(4.51) |
В случае ![]() мы имеем дело с туннелированием - частица «движется» внутри барьера с «мнимым» волновым вектором
мы имеем дело с туннелированием - частица «движется» внутри барьера с «мнимым» волновым вектором
|
|
|
(4.52) |
В этом случае тригонометрическая функция перейдет в гиперболическую
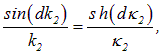
и из уравнения (4.49) следует выражение для коэффициента прохождения
|
|
|
(4.53) |
Если, как это обычно бывает, аргумент
![]()
то доминирует член с гиперболическим синусом, причем
![]()
Пренебрегая также предэкспоненциальными множителями, получаем уже знакомое выражение (4.34)
|
|
|
(4.54) |
Прохождение света через многослойную структуру
В этом разделе мы рассмотрим прохождение частицы над потенциальным барьером, составленным из 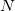 прямоугольных конечных барьеров шириной
прямоугольных конечных барьеров шириной 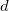 , причем межбарьерное расстояние всюду одинаково и равно
, причем межбарьерное расстояние всюду одинаково и равно  (рис. 4.22).
(рис. 4.22).
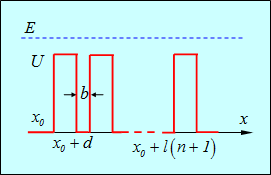
Рис. 4.22. Многослойная структура с периодом l = d + b, образованная N прямоугольными потенциальными барьерами шириной d и межбарьерным расстоянием b
В принципе задача о вычислении коэффициента прохождения ![]() через такой «составной» барьер может быть решена описанными выше способами. Сейчас нам важно только понять основной физический результат, так что нижеследующие формулы приводятся без вывода и только для справки. Выражение для коэффициента прохождения имеет вид
через такой «составной» барьер может быть решена описанными выше способами. Сейчас нам важно только понять основной физический результат, так что нижеследующие формулы приводятся без вывода и только для справки. Выражение для коэффициента прохождения имеет вид
|
|
|
(4.55) |
где ![]() — коэффициент прохождения через одиночный прямоугольный барьер, вычисленный выше (при
— коэффициент прохождения через одиночный прямоугольный барьер, вычисленный выше (при 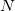 =1 получаем из (4.55)
=1 получаем из (4.55) ![]() ). Величина
). Величина
![]()
называется квазиволновым вектором (в отличие от волновых векторов частицы ![]() и
и ![]() она отмечена тильдой).
она отмечена тильдой).
В случае света мы используем для ![]() результат (4.50). Связь квазиволнового вектора с частотой падающего света и показателем преломления дается тогда выражением
результат (4.50). Связь квазиволнового вектора с частотой падающего света и показателем преломления дается тогда выражением
|
|
|
(4.56) |
где
|
|
|
(4.57) |
Наконец, входящие в (4.55) функции определены как
|
|
|
(4.58) |
Ясно, что для частот, при которых абсолютно прозрачен прямоугольный барьер ![]() будет прозрачен и наш составной барьер (
будет прозрачен и наш составной барьер ( ![]() в этом случае, как следует и из формулы (4.55)). В дополнение появятся и новые окна прозрачности. Здесь ситуация очень похожа на случай с дифракционной решеткой. Численное решение показано на рис. 4.23, где для конкретности мы положили
в этом случае, как следует и из формулы (4.55)). В дополнение появятся и новые окна прозрачности. Здесь ситуация очень похожа на случай с дифракционной решеткой. Численное решение показано на рис. 4.23, где для конкретности мы положили 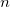 = 1,52,
= 1,52,  = 0,9d.
= 0,9d.
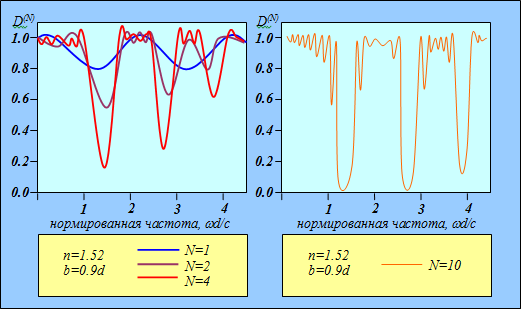
Рис. 4.23. Коэффициент прохождения в зависимости от нормированной частоты падающего света (энергии частицы) для малого (слева) и большого (справа) числа 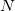
Левый рисунок представляет собой коэффициент прохождения для одного, двух и четырех барьеров, правый — для десяти барьеров. Последний случай, когда число барьеров велико ![]() представляет для нас особый интерес. Тенденции, обнаруживающиеся для
представляет для нас особый интерес. Тенденции, обнаруживающиеся для 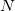 = 10, в пределе
= 10, в пределе
![]()
станут отчетливее. А именно: с ростом 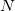 некоторые минимумы становятся глубже и шире, и в пределе значение коэффициента прохождения в них стремится к нулю. Наоборот, амплитуда колебаний
некоторые минимумы становятся глубже и шире, и в пределе значение коэффициента прохождения в них стремится к нулю. Наоборот, амплитуда колебаний ![]() при других частотах становится меньше, и коэффициент прохождения стремится к единице. Физическое объяснение этого явления заключается в том, что при выполнении определенных условий отраженные от концов прямоугольных барьеров волны взаимно компенсируют, гасят друг друга.
при других частотах становится меньше, и коэффициент прохождения стремится к единице. Физическое объяснение этого явления заключается в том, что при выполнении определенных условий отраженные от концов прямоугольных барьеров волны взаимно компенсируют, гасят друг друга.
Подчеркнем еще раз: для предельного случая периодической структуры
![]()
зависимость коэффициента прохождения
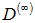
от частоты падающего света такова, что:
- имеются целые полосы частот, в которых
![]()
для таких частот составной барьер непрозрачен, свет этих частот полностью отражается от структуры;
- для других же частот, наоборот,
![]()
то есть для них барьер полностью прозрачен, отражения не происходит, и свет свободно распространяется в такой структуре (на этом явлении основано создание так называемых просветленных объективов).
Аналогичное явление происходит и в квантовой механике для частицы, движущейся в периодическом потенциальном поле. При некоторых значениях энергии частицы бесконечная периодическая последовательность потенциальных барьеров становится для нее совершенно непрозрачной, даже если энергия частицы превышает высоту барьера. При других энергиях, наоборот, периодическая потенциальная структура становится для частицы абсолютно прозрачной. Так возникают так называемые запрещенные и разрешенные энергетические зоны в кристалле, и мы с ними в свое время познакомимся поближе.