5.6. Принцип Паули и валентность элементов

Мы видели, что орбитальный момент импульса характеризуется азимутальным квантовым числом, принимающим целые значения. Собственный спиновый момент электрона характеризуется спиновым квантовым числом s, равным 1/2. Спин — фундаментальное квантовое свойство всех элементарных частиц. В соответствии со значением спинового квантового числа s частицы делятся на два класса: бозоны (целые s) и фермионы (полуцелые s). Другие значения s науке не известны. Примеры фермионов: электрон, мюон, нейтрино, кварки, частицы из трех кварков (протон, нейтрон). Примеры бозонов: фотон, недавно открытые частицы W^± и Z, частицы из двух кварков (p–мезоны и др.).

Бозоны и фермионы — это не имена собственные каких-то частиц, а названия целых семейств. Бозоны и фермионы подчиняются квантовым статистикам Бозе — Эйнштейна и Ферми — Дирака соответственно, которые мы рассмотрим позднее. Каждая микрочастица принадлежит одному из этих двух семейств и поменять принадлежность уже не в состоянии. В теории элементарных частиц замечено, что из фермионов построено вещество, а бозоны являются переносчиками фундаментальных взаимодействий.

Рис. 5.24. Шатьендранат Бо́зе или Бо́шу 1894–1974

Рис. 5.25. Энри́ко Фе́рми, 1901–1954

Если собрать вместе несколько бозонов, то они не мешают друг другу занять низшее энергетическое состояние и, следовательно, все там окажутся.

Поведение коллектива фермионов регулируется принципом Паули:

В применении к атому принцип Паули запрещает двум электронам иметь одинаковый набор квантовых чисел: состояния электронов должны отличаться значением хотя бы одного из них. Если бы принципа Паули не существовало, то у всех атомов в основном состоянии все электроны находились бы на нижнем энергетическом уровне и атомы различных элементов были бы до ужаса похожи друг на друга. Таким образом, известная нам химия, все разнообразие элементов и их свойств (в частности, гамма вкусовых ощущений, отличающая, скажем, вино от сыра) — следствия принципа Паули.

До сих пор мы в основном рассматривали только атом с одним электроном. Станем добавлять лишний электрон и, соответственно, увеличивать на единицу заряд ядра. Иными словами, совершим прогулку по таблице Менделеева. Введем понятия оболочки как совокупности уровней с одинаковыми главными квантовыми числами п и подоболочки (уровни данной оболочки с одинаковыми l). Традиционные обозначения оболочек следующие

Число уровней в оболочке мы фактически уже подсчитали: оно равно кратности вырождения по m и l, умноженной на 2, в соответствии с двумя возможными направлениями спина электрона. Таким образом, согласно принципу Паули, оболочка может вместить  электронов, а подоболочка — 2(2l + 1) электронов (число различных значений n, удвоенное по той же причине). Итак, состояния электронов в атоме различаются квантовыми числами  и , и, по принципу Паули, лишь один электрон может иметь данный конкретный набор квантовых чисел.

Напомним: три квантовых числа  отражают трехмерность пространства,  — внутренние свойства электрона.

Порядок заполнения уровней в многоэлектронных атомах определяется энергией уровней с учетом влияния заполненных оболочек. Нижние оболочки частично экранируют заряд ядра, что ведет к некулоновскому полю для высших оболочек. Этим объясняется зависимость энергии уровней от квантового числа l. Чем больше l (для электронов одной оболочки), тем дальше находится электрон от ядра и тем слабее его связь с ядром, то есть такой уровень лежит выше. При больших моментах (состояния d, f и т. д.) энергетические уровни данной оболочки близки или даже выше s-подуровней следующей оболочки. В целом заполнение идет в таком порядке (случаются небольшие отклонения):

||1s||2s, 2p||3s, 3p||4s, 3d, 4p||5s, 4d, 5p||6s, 4f, 5d, 6p|| и т.д.

В этом ряду знаком || отделены периоды таблицы Менделеева. В соответствии с полученными формулами для числа уровней в зависимости от n и l, первый период содержит 2 элемента, второй и третий — по 8, а четвертый и пятый — по 18 элементов. Здесь «вклиниваются» заполнения d-подоболочек (по 10 элементов — переходные металлы). В шестом периоде добавляется заполнение f-подоболочки (14 элементов — лантаниды) и т. д.

Рис. 5.26. Схема заполнения одночастичных состояний в атомах

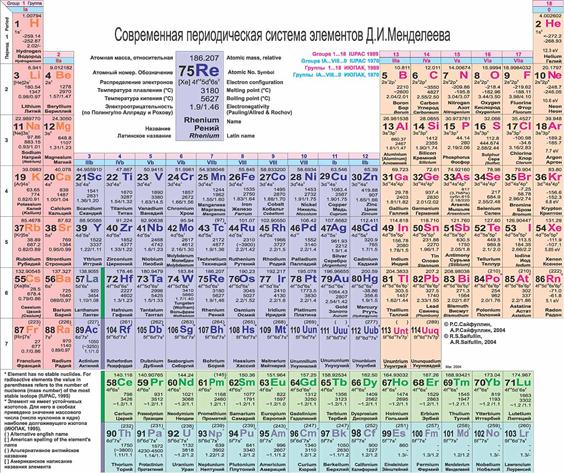
Рис. 5.27. Современная периодическая система элементов Д.И. Менделеева

Химические свойства зависят в основном от строения внешней электронной оболочки (валентных электронов). Отсюда и вытекает периодичность повторения свойств элементов. Так, у благородных газов заполнены внешние s- и p-подоболочки из 8 электронов. У элементов первой группы (щелочные металлы) на внешней оболочке имеется всего один электрон, а галогенам (VII группа) не хватает одного электрона для заполнения внешней p-подоболочки. Все эти рассуждения хорошо знакомы по курсу химии, но они носят качественный характер. Как известно, валентность элемента определяется не столько количеством электронов, сколько степенью легкости, с которой их можно вырвать из атома. Понятно, что внешние электроны оторвать легче, но хотелось бы получить хоть какой-нибудь количественный критерий. Таким критерием может служить потенциал ионизации, пропорциональный энергии, которую необходимо затратить, чтобы удалить электрон из атома. Расчет сложных атомов непрост, но в целом таблица Менделеева объясняется квантовой механикой. Мы ограничимся лишь самыми простыми атомами и точные расчеты заменим количественными оценками. Экспериментальные результаты представлены на рис. 5.28.

Рис. 5.28. Потенциал ионизации для элементов от водорода до урана. Ясно видна периодичность свойств элементов:
пики потенциала ионизации случаются для благородных газов, минимумы — для щелочных металлов

Эффективный заряд ядра, оценки потенциала ионизации и закон Мозли

Мы в деталях изучили энергетические уровни водородоподобных атомов, описываемые формулой Бора

Для более сложных систем со многими электронами эта формула неверна, но мы будем ее использовать, вводя поправку на экранировку ядра электронами путем замены заряда ядра Z нa некий эффективный заряд . Большой точности сравнения с экспериментальными данными так не добиться, но мы удовлетворимся совпадением по порядку величины.

Водород. Заряд ядра Z = 1, экранировки нет, в основном состоянии n = 1. Энергия основного уровня , минимальная энергия электрона, вырванного из атома, равна нулю. Следовательно, ионизационный потенциал U — это абсолютное значение энергии основного состояния, выраженное в вольтах: U = 13,6 эВ. Эта величина будет служить нам ориентиром, позволяющим не заблудиться в энергетической шкале микромира.

Положительный ион гелия. Ион  отличается от водорода только удвоенным зарядом ядра: Z = 2. Отсюда U = 13,6·4 = 54,4 эВ В.

Гелий. Нейтральный атом гелия в основном состоянии имеет два электрона на нижней оболочке (n = 1), отличающиеся проекциями спинов. Представим себе такую картину. Когда второй электрон находится дальше от ядра, чем первый, то заряд ядра от него экранируется и равен (с его «точки зрения») единице. Когда же второй электрон располагается к ядру ближе первого, то «видимый» им заряд ядра равен двум. Оба электрона равноправны, так что описанные ситуации равновероятны. Поэтому для оценки эффективного заряда у ядра мы возьмем среднее арифметическое:

Конечно, электрон не может полностью экранировать ядро от своего партнера. Конечно, надо принять во внимание энергию кулоновского отталкивания электронов. И все же получающаяся оценка не столь плоха:

Эксперимент дает

Бросается в глаза огромная величина ионизационного потенциала у гелия (самый большой в таблице Менделеева). Инертность гелия — прямое следствие этого факта.

Дважды ионизованный атом лития . Водородоподобная система с Z = 3. Поэтому

Ион лития. Ион  подобен атому гелия, но для него эффективный заряд ядра на единицу больше:

Отсюда

Эксперимент дает

Литий. Третий электрон в нейтральном атоме лития располагается на второй оболочке — уровне с n = 2. По этой причине два внутренних электрона почти полностью экранируют от него две единицы заряда ядра:

Отсюда

Эксперимент дает

Эти оценки очень показательны: насколько легче (в сравнении с водородом) оторвать от лития один электрон и как трудно удалить последующие. Поэтому литий — одновалентен.

Бериллий. Ионы  и  аналогичны водороду и гелию и имеют огромные потенциалы ионизации. Ион  похож на литий, но у него на единицу больше эффективный заряд ядра, «видимый» третьим электроном:

Получаем

Эксперимент дает 18,2 эВ. Это значение не намного больше потенциала ионизации атома водорода и заведомо много меньше потенциала ионизации иона . В нейтральном атоме Be на второй оболочке помещаются два электрона. Система похожа на ион , но эффективный заряд ядра на единицу больше:

Отсюда

Экспериментальное значение 10,4 эВ. Отсюда вывод: поскольку первые два электрона вырвать из атома бериллия гораздо легче, чем последующие, то бериллий — двухвалентен.

Понятие эффективного заряда ядра полезно также при рассмотрении свойств так называемого характеристического рентгеновского излучения, возникающего при переходе внешних электронов на свободное место на внутренних оболочках. Как мы выяснили, для электронов на КК оболочке

Рис. 5.29. Происхождение характеристического излучения. При столкновении с электроном в атоме мишени образуется вакансия во внутренней электронной оболочке. Эту вакансию заполняет электрон из другой оболочки. При этом излучается рентгеновский квант

Видео 5.4. Установка для исследования рентгеновского излучения.

Видео 5.5. Ослабление рентгеновского излучения различными веществами.

Видео 5.6. Коротковолновая граница спектра тормозного излучения.

Видео 5.7. Характеристическое рентгеновское излучение.

Пример. Для меди Сu Z = 29 и

При переходе внешних, далеких от ядра электронов с энергией, почти равной нулю, испускается фотон с энергией

Длина волны такого фотона

В 1913 г. был установлен закон Мозли, связывающий частоту n характеристического рентгеновского излучения элемента и его атомный номер Z:

где  — Ридберг, n — главное квантовое число оболочки, на которую совершается переход, а  — некая постоянная. В этом законе легко теперь увидеть проявление экранирования ядра, то есть влияние на отдельный электрон атома всех остальных электронов. Исторически закон Мозли окончательно подтвердил, что свойства элемента зависят от атомного номера Z, а не от атомной массы. Это устранило последние сомнения в правильности расположения элементов в периодической системе.

Рис. 5.30. Закон Мозли подтвердил правильность размещения элементов в таблице Д.И. Менделеева и содействовал выяснению физического смысла Z

Видео 5.8. Экспериментальная проверка закона Мозли.

Рис. 5.31. Ге́нри Гвин Дже́фрис Мо́зли, 1887–1915

Электронная конфигурация атомов

Для атома любого элемента мы можем указать его основную электронную конфигурацию. Теперь познакомимся с двумя правилами, позволяющими узнать для основного состояния каждого атома значение его суммарных моментов: спинового S, орбитального L и полного J.

Первое правило (правило Хунда)

Второе правило

Правило Хунда является эмпирическим (то есть не выведенным из теории, а установленным экспериментально); второе правило выводится из него и из полученной выше формулы (5.19) для скалярного произведения S·L. Для облегчения применения правила Хунда полезно запомнить, что:

• надо рассматривать только незаполненную электронную подоболочку, так как моменты электронов в заполненных подоболочках взаимно компенсируются и суммарные моменты заполненных подоболочек всегда равны нулю;
• значения S и L одинаковы для двух подоболочек, из которых одна имеет столько электронов, сколько не хватает для заполнения другой.

Для примера применения указанных правил рассмотрим атом серы. Его атомный номер Z = 16 и, следовательно, основная электронная конфигурация имеет вид 1s² 2s² 2p⁶ 3s² 3p⁴. Индексы справа вверху обозначают числа электронов в указанных состояниях. Видим, что незаполненной остается последняя подоболочка, на которой находятся четыре электрона с орбитальными моментами, равными единице. При данном L = 1 , согласно принципу Паули, параллельными могут быть лишь спины трех электронов, отличающихся значениями m = –1, 0, +1. Спин четвертого электрона должен быть направлен в противоположную сторону, и потому максимально возможное значение суммарного спина для данной конфигурации равно

При этом значении S сумма проекций орбитальных моментов электронов с одинаково направленными спинами равна нулю, следовательно, максимально возможное значение проекции суммарного орбитального момента определяется четвертым электроном и равно единице. Поэтому L = 1. Так как внешняя подоболочка заполнена более чем наполовину, то J = L + S = 2. Мы пришли к выводу, что основным состоянием атома серы является .

Для сравнения найдем основное состояние атома кремния (Z = 14). От атома серы он отличается тем, что на внешней подоболочке у него находятся два, а не четыре p-электрона. Для ее заполнения не хватает четырех электронов, то есть столько, сколько их имеется у серы. Поэтому для атома кремния получаем те же значения S = 1 и L = 1. Внешняя подоболочка заполнена менее чем наполовину, откуда J = |L – S| = 0. Поэтому основным состоянием кремния является .

Рис. 5.32. Фридрих Хунд, 1896–1997