7.6. Статистика Ферми — Дирака

Бозоны и фермионы имеют совершенно разные статистические свойства, то есть по-разному ведут себя в коллективе себе подобных. Кроме непосредственного силового взаимодействия между частицами, имеется специфически квантовое, обменное взаимодействие: это не какие-то дополнительные силы или поля — одни частицы влияют на поведение других одним своим присутствием. Эти эффекты ощущаются частицами, если они находятся друг от друга на расстояниях, меньших или порядка длины волны де Бройля . При высоких температурах энергии частиц велики и  мало — это область классической физики. При низких температурах  возрастает и квантовые эффекты доминируют.

Рассмотрим систему одинаковых фермионов с энергиями  в состоянии i (где i обозначает набор квантовых чисел, включая спин). Обозначим через  число частиц в состоянии i. Основной принцип статистической физики (классической и квантовой) формулируется исследующим образом:

Здесь C — нормировочная постоянная, а  — химический потенциал. Этот параметр появляется всегда при фиксированном числе частиц в системе, которое равно

где сумма берется по всем состояниям. По сути дела, уравнение (7.38) — это обобщение известного распределения Больцмана. Из принципа Паули следует, что для фермионов  могут принимать лишь значения 0 и 1 — в данном состоянии i может быть либо одна частица, либо ни одной вообще.

Из всего набора возможных состояний системы проследим за каким-то конкретным состоянием k с энергией . С некой вероятностью

в нем может не оказаться ни одной частицы (). С вероятностью

в нем окажется одна частица (). При записи формул (7.39), (7.40) мы использовали общее выражение (7.38) для вероятности

.

Поскольку третьего не дано, должно выполняться условие нормировки

откуда следует

Значит, среднее число частиц

в состоянии k получается равным

Формула (7.42) является основой квантовой статистики Ферми — Дирака. При высоких температурах получаем

то есть равномерное распределение частиц по состояниям. Если число частиц N в системе фиксировано, то химический потенциал  определится из условия

Подчеркнем также, что согласно (7.42) среднее число частиц в данном состоянии всегда не превышает единицы. Это — прямое следствие принципа Паули.
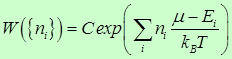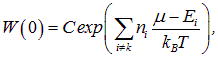
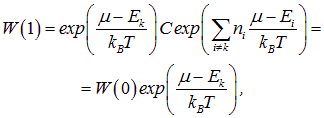
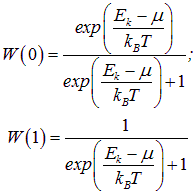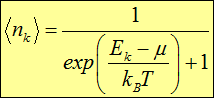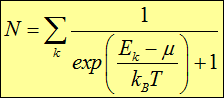