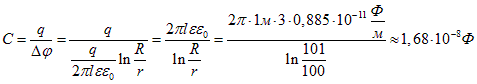(1)
Ёмкость конденсатора по определению равна частному заряда и разницы потенциалов на его обкладках:
|
(1) |
Разность потенциалов между двумя точками равна:
Следовательно, в нашем случае:
|
(2) |
Найдём теперь напряжённость электрического поля между обкладками диэлектрика. Для этого применим теорему Гаусса для вектора электрического смечения, которая гласит, что поток электрического смещения через замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, делённой на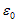 
:
|
(3) |
Вектор электрического смещения равен:
|
(4) |
Посчитаем поток через поверхность коаксиального конденсатору цилиндра, находящегося между обкладками конденсатора.
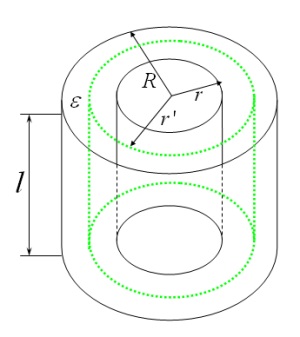
Учитывая, что векторы 
и 
сонаправлены, из (3) и (4) находим:
,
где 
— заряд на обкладках конденсатора
|
(5) |
Из (2) и (5) находим:
|
(6) |
Итак, из (1) и (6) получаем:
