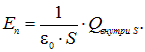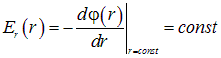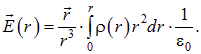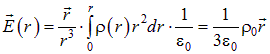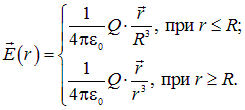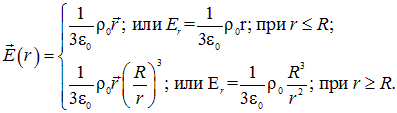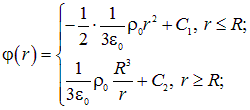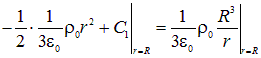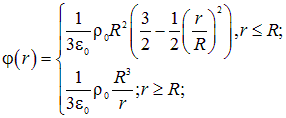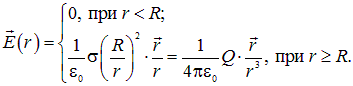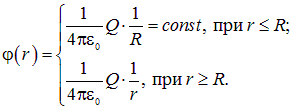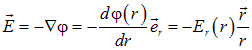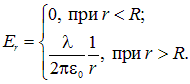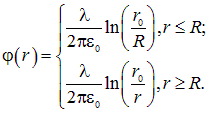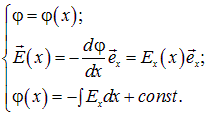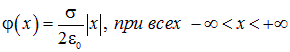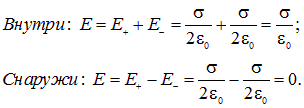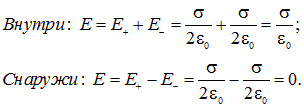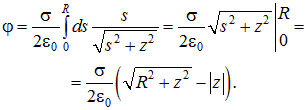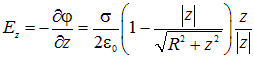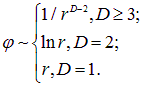1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля

Теорема Гаусса для вектора

может быть успешно использована как эффективный инструмент расчета напряженности и потенциала электрического поля некоторого распределения заряда, когда стоящий слева интеграл может быть превращен в произведение площади поверхности, по которой производится интегрирование, на величину нормальной к поверхности составляющей вектора , то есть когда

Вполне очевидно, что для расчета вектора этого будет достаточно, во-первых, когда вектор перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Её форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что

вовсе не вытекает, что и

в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства — отдельное требование.

Из сказанного выше вытекает, что теорема Гаусса в состоянии быстро и просто привести к результату (вектору ) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что на этих поверхностях. Если всё это имеет место, то решение выглядит следующим простым образом:

(1.36)

Остается выбрать поверхность

согласно симметрии распределения заряда и вычислить заряд внутри

Сферическая симметрия

При сферически симметричном распределении заряда поле, создаваемое им, также сферически симметрично. Векторные (и скалярные) поля с такой симметрией принято также называть центральными полями. Центрально симметричное поле в общем случае можно записать в виде

Здесь — радиус-вектор, начинающийся в центре симметрии поля r — его модуль, — радиальная составляющая напряженности поля, зависящая только от расстояния до его центра симметрии. Потенциал такого поля зависит только от и

(1.37)

И, кроме того, как следует из , при произвольной нормировке потенциал поля имеет вид

(1.38)

Таким образом, условия применимости выполнены и мы можем воспользоваться этим соотношением.

Возьмем в качестве эквипотенциальную сферическую поверхность некоторого текущего радиуса r, её площадь . Виду предполагаемой непрерывности распределения заряда, для используем выражение:

где — объёмная плотность заряда. Опять-таки, учитывая сферическую симметрию распределения заряда — зависит только от , в качестве элемента объёма естественно взять бесконечно тонкий сферический слой с внутренним радиусом и внешним радиусом . Объём такого слоя , в результате получаем

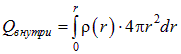Окончательно, для любого сферически симметричного распределения заряда, когда , получаем

(1.39)

Продолжение вычислений требует конкретизации вида зависимости плотности заряда от модуля радиус-вектора .

Поле однородно по объёму заряженного шара

Равномерное по объёму шара радиуса распределение заряда (рис. 1.41) означает, что его плотность заряда имеет вид

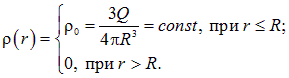
Рис. 1.41. Силовые линии электрического поля однородно заряженного шара

Не следует забывать, что по условию вне шара зарядов нет.

Поскольку в точке плотность заряда меняется скачком: предел «слева» отличен от нуля , а предел «справа» равен нулю , вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса (она лежит внутри шара), а потом для сферической поверхности радиуса (она охватывает шар). В первом случае

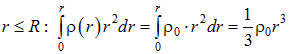Соответственно, поле

(1.40)

растет линейно с ростом расстояния до центра шара, что объясняется просто: площадь поверхности , а заряд внутри неё

Во втором случае интеграл «обрезается сверху» при :

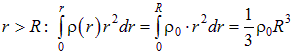
и поле

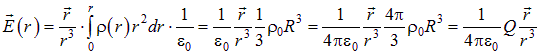В последнем выражении учтено, что , где — полный заряд шара. Таким образом, вне шара его поле есть поле точечного заряда равного полному заряду шара и помещенного в центр этого шара:

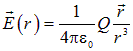Оба выражения можно объединить в одну формулу. Если использовать полный заряд шара , получим:

(1.41)

Если вместо полного заряда шара использовать в качестве параметр плотность заряда , эти формулы приобретут следующий вид (рис. 1.42):

(1.42)

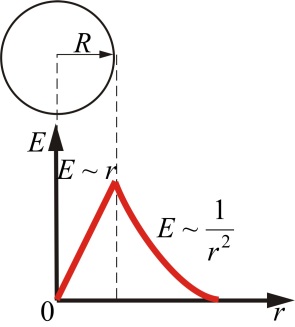
Рис. 1.42. Распределение напряженности электрического поля однородно заряженного шара

Формулы и выражают одну и ту же зависимость, их удобство определяется тем, какие параметры заданы: или . Из этих формул наглядно видно, что на поверхности шара напряженность поля непрерывна, то есть не имеет разрыва. Это обусловлено тем, что в данном случае разрыв плотности заряда на поверхности шара первого рода — конечной величины: с на нуль. Поэтому, как в , так и в в верхней и в нижней формулах поставлены знаки нестрогих неравенств. В каких случаях напряженность поля может терпеть разрыв, будет ясно из следующего примера.

Потенциал поля легко найти, подставив, например, из в и выполнив интегрирование. Получаем:

(1.43)

где и — постоянные интегрирования, которые находятся из следующих соображений. Константа определяется из условия нормировки, например, на нуль на бесконечности

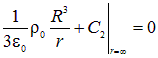
Откуда . Константа определяется из условия непрерывности потенциала на поверхности шара, то есть при :

(1.44)

или

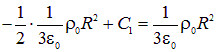
откуда

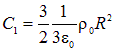
Отметим, что требование непрерывности потенциала нередко называют «сшивкой» двух решений на границе раздела. В данном случае это граница раздела двух областей: областью, где есть заряд (внутри шара), и областью, где его нет (вне шара). Уже сейчас можно отметить, что потенциал непрерывен во всех случаях, кроме одного: так называемого «двойного слоя». Представьте поверхность, по одной стороне которой с плотностью распределен положительный заряд, а по другой стороне которой с плотностью распределен отрицательный заряд. Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.

Подставляя полученные значения констант интегрирования в , запишем окончательный результат в виде

(1.45)

При такой нормировке потенциал в центре шара отличен от нуля и равен

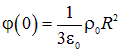Полученные результаты иллюстрирует приведенный ниже рисунок 1.43.

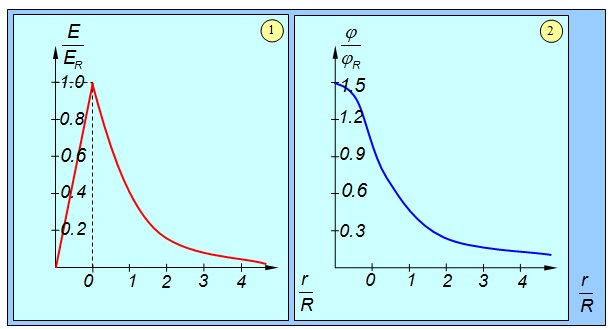
Рис. 1.43. Напряженность (1) и потенциал (2) электрического поля равномерно заряженного шара радиусом R в единицах напряженности и потенциала на его поверхности (r = R)

Поле равномерно заряженной сферической поверхности

В данном случае равномерного распределения заряда по сферической поверхности, как и в предыдущем, имеет место сферическая симметрия, поэтому общие формулы, полученные выше, применимы и здесь. Однако относиться к ним необходимо с известной осторожностью по следующей причине. Входящая в правую часть объемная плотность заряда ведет себя в данном случае следующим интересным образом:

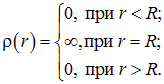
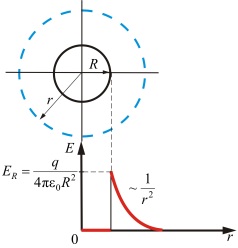
Рис. 1.44. Напряженность электрического поля равномерно заряженной сферы

Действительно, заряд имеется только на поверхности, то есть при , всюду внутри, то есть при и всюду снаружи, то есть при зарядов нет. То, что объемная плотность заряда в точках поверхности обращается в бесконечность (+∞ в случае положительного заряда и –∞ в случае отрицательного) можно показать следующим образом. На рисунке рядом изображен участок некоторой поверхности, по которой с поверхностной плотностью распределен заряд. Для определения величины объёмной плотности заряда в некоторой точке поверхности рассмотрим цилиндр (рис. 1.45), верхнее основание которого находится над поверхностью, а нижнее — под поверхностью. Площадь оснований цилиндра равна , высота — , объём . Заряд внутри цилиндра , объёмная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объёма «физически бесконечно малого»). Получаем

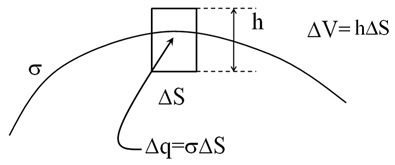
Рис. 1.45. Плотность заряда на поверхности

Важно, что плотность на поверхности равна бесконечности. Функции такого рода (везде, кроме одной точки — нуль, а в этой единственной точке — бесконечность) относятся к классу так называемых обобщенных функций, называются функциями Дирака в честь физика Дирака, впервые введшего в обиход физики такую функцию для удовлетворения нужд квантовой механики. Мы не будем здесь подробно исследовать и использовать в расчетах такого рода функции. Наша цель показать, что рассмотрение формально бесконечно тонких заряженных поверхностей приводит к появлению у объёмной плотности заряда разрывов (бесконечных), что, в свою очередь, порождает бесконечные разрывы на такой заряженной поверхности у напряженности электрического поля. Подчеркнем, что потенциал поля при этом остается непрерывным.

Выход из положения прост. При всех используем первую из формул с , получаем, что всюду внутри однородно заряженной сферической оболочки поле отсутствует: . При всех справедлива вторая формула из . Как и в случае однородно по объёму заряженного шара, вне однородно заряженной сферической оболочки, её поле есть поле точечного заряда, помещенного в центр этой оболочки и равного её полному заряду. В данном случае, разумеется .

Окончательный результат такой:

(1.46)

На самой сферической поверхности напряженность поля в этом случае терпит разрыв. Зависимость радиальной компоненты поля от расстояния до центра сферической поверхности показана на рис. 1.46.

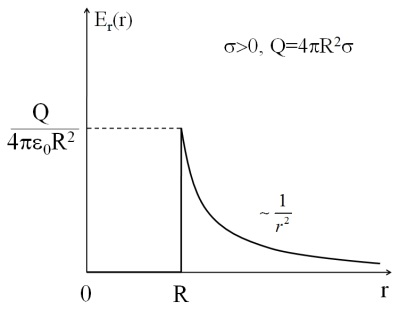
Рис. 1.46. Зависимость поля от расстояния до центра сферической оболочки

Зависимость потенциала от расстояния до центра сферической оболочки можно получить, интегрируя . При нормировке на нуль на бесконечности результат выглядит следующим образом:

(1.47)

Зависимость показана на рис. 1.47.

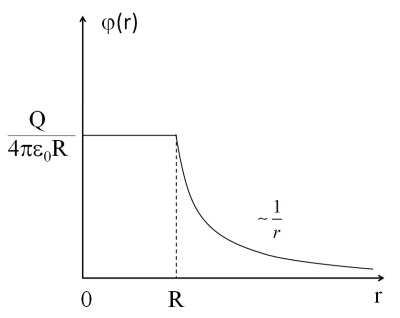
Рис. 1.47. Потенциал равномерно заряженной сферы

Однородное (равномерное) распределение заряда по бесконечно длинной цилиндрической поверхности (рис. 1.48) обладает цилиндрической, трансляционной и зеркальной симметрией. Это означает следующее. При повороте такого распределения заряда вокруг оси цилиндрической поверхности на любой угол оно совпадает само с собой. При сдвиге (переносе, трансляции) такого распределения заряда на любое расстояние вдоль оси симметрии оно также совпадает само с собой. И, наконец, если через любую точку на оси симметрии провести плоскость перпендикулярную к оси, и отразить в этой плоскости как в зеркале «верхнюю» часть распределения заряда, то отражение «верхней» части совпадет с «нижней» и наоборот, отражение «нижней» совпадет с «верхней». Другими словами, это распределение заряда инвариантно относительно указанных преобразований. Следовательно, и создаваемое этим распределением заряда электрическое поле должно быть инвариантно (совпадать само с собой) при указанных преобразованиях.

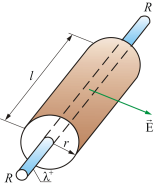
Рис. 1.48. Бесконечно длинная цилиндрическая поверхность

Введем цилиндрическую систему координат: ось направим по оси симметрии, — расстояние до оси симметрии, — азимутальный угол, угол поворота вокруг оси симметрии, — по-прежнему потенциал поля.

Из свойств симметрии вытекает, что потенциал поля не может зависеть ни от координаты — нарушится трансляционная симметрия, ни от координаты — нарушится осевая (цилиндрическая) симметрия. Остается только зависимость от — расстояния до оси цилиндра. Таким образом:

(1.48)

Соответственно

(1.49)

вектор напряженности электрического поля направлен по радиальным прямым, перпендикулярным оси симметрии (рис. 1.49), и его величина зависит только от расстояния до оси. Потенциальные поверхности представляют собой цилиндры соосные с заряженной цилиндрической поверхностью.

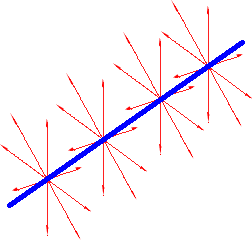
Рис. 1.49. Вектор напряженности электрического поля направлен по радиальным прямым

Используя эти обстоятельства, будем интегрировать в левой части теоремы Гаусса по замкнутой поверхности цилиндра с радиусом основания и высотой , соосного с рассматриваемой, заряженной цилиндрической поверхностью радиуса . Поток через основания цилиндра равен нулю ввиду того, что на основаниях , а поток через его боковую поверхность равен произведению на её площадь: . Соответственно, суммарный (через всю замкнутую поверхность рассматриваемого цилиндра) поток вектора равен

(1.50)

При , находящийся внутри цилиндра заряд, равен

где — линейная плотность заряда численно равная заряду, приходящемуся на единицу длины цилиндрической поверхности. Согласно теореме Гаусса

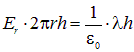
откуда для получаем

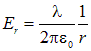При внутри цилиндра, через поверхность которого вычисляется поток вектора , зарядов нет, и потому поле равно нулю. Объединяя эти два результата, получаем окончательно (рис. 1.50):

(1.51)

Ввиду поверхностного характера распределения заряда (см. подробнее предыдущий расчёт) на самой заряженной поверхности, то есть при радиальная компонента поля терпит разрыв.

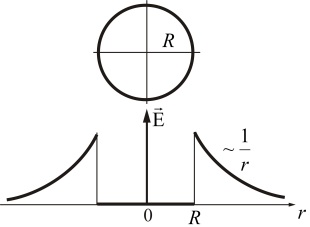
Рис. 1.50. Напряженность электрического поля равномерно заряженной цилиндрической поверхности

Интегрирование (1.51) (см. также (1.49)), требование непрерывности потенциала при , и нормировка , приводят к следующей зависимости потенциала от расстояния до оси цилиндрической поверхности:

(1.52)

В данном случае, когда бесконечно большой по модулю заряд распределен по бесконечно длинному цилиндру, относится к тем случаям, когда нормировка на нуль на бесконечности лишена смысла. Как видно из (1.52), зависимость потенциала от расстояния до оси логарифмическая, нормировка на нуль на бесконечности, на языке формул (1.52), означает, что , но, тогда потенциал будет бесконечно большим по модулю на любом конечном расстоянии от оси заряженной поверхности, что лишено смысла. Выбор того конечного расстояния от оси симметрии, на котором удобно потенциал считать равным нулю трудностей не вызывает и обусловлен спецификой задачи. Например, ничто не мешает положить , тогда потенциал всюду внутри и на самой заряженной поверхности будет равен нулю.

Поле бесконечной равномерно заряженной плоскости

Пусть поверхностная плотность заряда равна . Такое распределение заряда по бесконечной плоскости характеризуется тем, что его вид не зависит от: а) поворота на любой угол вокруг любой оси перпендикулярной плоскости, б) сдвига на любое расстояние вдоль прямой лежащей в плоскости и любого направления. Наконец, в) отражение данного распределения заряда в зеркале, совпадающем с самой плоскостью, оставит его неизменным.

Из анализа симметрии достаточно очевидно, что потенциал в любой точке вне плоскости может зависеть только от расстояния от этой точки до плоскости. Направим ось декартовой системы координат перпендикулярно плоскости, а оси и пусть принадлежат самой плоскости, тогда

(1.53)

Причем, в силу зеркальной симметрии, поле «перед» плоскостью отличается от поля «за» плоскостью только направлением вектора . Это означает, что зависимость от должна быть нечетной, а зависимость потенциала от должна быть четной.

В силу этих соображений возьмём замкнутую поверхность — ту, для которой будем писать теорему Гаусса, — следующего вида (рис 1.51).

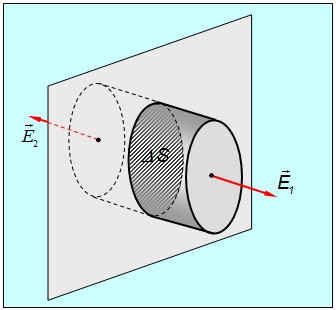
Рис. 1.51. Электрическое поле заряженной плоскости

Это цилиндр с боковой поверхностью перпендикулярной плоскости и с основаниями параллельными плоскости. Высота цилиндра , площадь оснований . Учитывая нечетность зависимости , основания цилиндра удобно расположить на одинаковом расстоянии от плоскости, тогда вклад оснований в поток будет одинаков. Напряженность поля на основаниях, во-первых, им перпендикулярна, во-вторых, сонаправлена с внешней нормалью, в-третьих, она одинакова во всех их точках по абсолютной величине

Вклад в поток вектора от боковой поверхности равен нулю, так как на боковой поверхности .

Поэтому полный поток через всю замкнутую цилиндрическую поверхность равен

(1.54)

Внутри рассматриваемой цилиндрической поверхности находится заряд

где — плотность заряда на плоскости. По теореме Гаусса

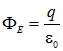следовательно, модуль напряженности поля заряженной плоскости равен

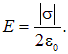
Подчеркнём, что результат очевидным образом не зависит от того, на каком расстоянии от плоскости расположены основания рассмотренного цилиндра. Отсюда следует, что с каждой стороны от плоскости создаваемое ею электрическое поле однородно.

Используя введенную ранее ось перпендикулярную заряженной плоскости, поле с обеих сторон от плоскости можно описать одной формулой, пригодной при любом знаке заряда на плоскости

(1.55)

Здесь — орт оси .

Интегрируя с учетом

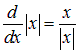для зависимости от потенциала поля плоскости нетрудно получить:

(1.56)

Потенциал в нормирован условием . Здесь, как и в примере с бесконечно длинной заряженной цилиндрической поверхностью, потенциал растет при удалении на бесконечность, поэтому нормировка на нуль на бесконечности лишена смысла.

Силовые линии поля заряженной плоскости показаны на рис. 1.52 и 1.53.

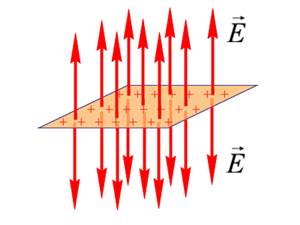
Рис. 1.52. Поле положительно заряженной плоскости

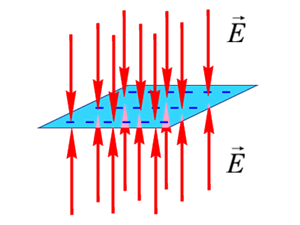
Рис. 1.53. Поле отрицательно заряженной плоскости

Поле плоского конденсатора

Определим напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными однородно и разноименно. Плотности заряда на плоскостях по модулю одинаковы и равны, соответственно: и (идеальный плоский конденсатор). С помощью рис. 1.54 нетрудно сообразить, что в зазоре между плоскостями, создаваемые ими поля направлены в одну сторону, поэтому внутри суммарное поле в два раза больше поля от каждой из плоскостей. Снаружи от плоскостей создаваемые ими поля направлены в противоположные стороны, соответственно, суммарное поле от обеих плоскостей равно нулю (рис. 1.55).

(1.57)

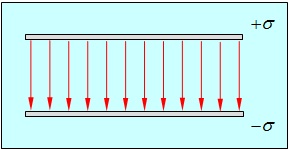
Рис. 1.54. Электрическое поле плоского конденсатора

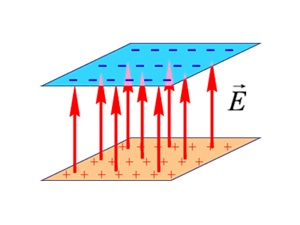
Рис. 1.55. Электрическое поле разноименно заряженных плоскостей

(1.58)

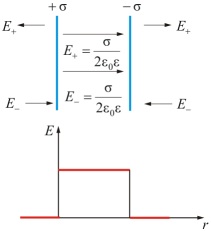
Рис. 1.56. Напряженность электрического поля разноименно заряженных плоскостей

В Дополнении 6 разобран пример с движением заряженной частицы в постоянном электрическом поле.

Потенциал поля заряженного диска

Как уже не раз отмечалось, зная потенциал поля точечного заряда и используя принцип суперпозиции, в принципе всегда, можно вычислить потенциал поля, создаваемого любым распределением зарядов.

Найдем для примера потенциал электрического поля, создаваемого на оси тонкого диска радиуса R, равномерно заряженного с поверхностной плотностью заряда (рис. 1.57). В силу осевой симметрии в точках на оси две перпендикулярных к оси составляющих напряженности поля равны нулю: , остается найти — составляющую поля, направленную вдоль оси.

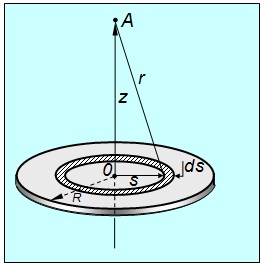
Рис. 1.57. Вычисление потенциала на оси заряженного диска

Выделим на диске кольцо радиусом s и шириной ds (заштриховано на рис. 1.57). Площадь кольца равна и потому на нем сосредоточен заряд

Поскольку все элементы кольца находятся на одинаковом расстоянии

от точки наблюдения А, то потенциал , создаваемый кольцом в точке А, дается все той же формулой с заменой в ней на :

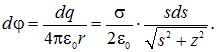
Полный же потенциал поля, создаваемый всем диском в точке A, равен сумме потенциалов от всех возможных колец с радиусами s, где 0 < s < R

(1.59)

При больших расстояниях от центра диска квадратный корень можно разложить в ряд, ограничившись первыми двумя членами разложения

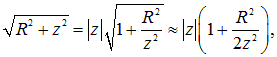
тогда формула упрощается и, как и должно быть, превращается в формулу для потенциала точечного заряда

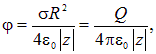
где — полный заряд диска

Используя связь напряженности поля с потенциалом , можно найти напряженность поля на оси диска

(1.60)

Закон Кулона и размерность пространства

Пространство, в котором мы живем, имеет три измерения. Иными словами, нужны три координаты (например, в декартовой или в сферической системах) для задания положения точки А (рис. 1.58). Оказывается, число 3 тесно связано с формой закона Кулона. Мы видели, что теорема Остроградского — Гаусса следует из закона Кулона. Верно и обратное, закон Кулона можно вывести из теоремы Остроградского — Гаусса. Но эта теорема носит более общий характер, чем закон Кулона. В частности, она применима к пространствам с размерностью , где не обязательно должно быть равно трем.

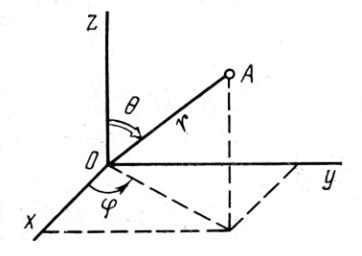
Рис. 1.58. Декартовая и сферическая системы координат

В самом деле, теорема в сущности утверждает, что силовые линии начинаются и заканчиваются на зарядах или уходят в бесконечность. Размерность пространства не играет здесь роли. Поэтому давайте предположим, что мы живем в пространстве с какой-то размерностью и посмотрим, какой будет физика в этом странном мире. Возьмем точечный заряд и мысленно окружим его сферой радиусом Прежде чем продолжать знакомство с мерной физикой, условимся о терминологии.

Объем сферы будет измеряться в единицах подобно тому, как в нашем мире мы измеряем объем в . Так, в двумерном пространстве роль объема играет наша площадь. Действительно, сфера — это геометрическое место точек пространства, равноудаленных от центра. Согласно этому определению, двумерная сфера — это окружность радиусом двумерные существа считали бы ее объемом то, что мы воспринимаем как площадь круга В этом параграфе мы будем называть объемом сферы в мерном пространстве ту величину, которая пропорциональна Аналогично, площадь поверхности мерной сферы пропорциональна В двумерном пространстве это — длина окружности и именно ее двумерные существа воспринимали бы как площадь поверхности. С другой стороны, площадь поверхности в четырехмерном мире — это наши трехмерные объемы.

Итак, площадь сферы в мерном мире пропорциональна (коэффициент пропорциональности сейчас нам не важен). Поток вектора напряженности электрического поля в таком мире пропорционален и должен быть пропорционален также величине электрического заряда внутри сферы (теорема Остроградского — Гаусса). Отсюда получаем, что

(10.49)

где — некий коэффициент пропорциональности. Аналогичное выражение справедливо для гравитационного поля в мерном мире.

При получаем отсюда закон обратных квадратов (закон Кулона). При находим На самом деле мы уже знакомы с таким поведением электрического поля. Именно такой закон (10.17) мы вывели для поля бесконечного заряженного цилиндра. Если как следует подумать и вспомнить расположение силовых линий цилиндра, то станет ясно, что ничего не зависит от координаты вдоль оси цилиндра. Таким образом, эта система имитирует электрическое поле в двумерном мире. Теперь легче понять, что заряженная плоскость имитирует точечный заряд в одномерном мире: все зависит только от одной координаты — расстояния до плоскости. Но мы нашли выше, что электрическое поле от этого расстояния не зависит. И из формулы (10.49) при также следует, что напряженность то есть постоянна. В четырехмерном же мире закон Кулона принял бы форму Таким образом, закон обратных квадратов является прямым следствием трехмерности нашего мира.

Из выражения (10.49) следует поведение потенциала в мерном мире:

(10.50)

Эти формулы являются следствием того, что дифференцирование потенциала (операция grad) должно дать выражение для напряженности электрического поля.

Отсюда следуют любопытные выводы. Поскольку в одно- и двумерном мирах потенциалы растут на бесконечности, нужна бесконечно большая работа, чтобы развести два притягивающихся заряда. Это означает, что в мирах малой размерности возможно лишь финитное движение двух притягивающихся тел (зарядов, масс). Напомним, что финитным называется движение в ограниченной области пространства. Поэтому в мирах с нельзя ионизировать атом, нельзя запустить спутник за пределы Солнечной системы и т. п. В таком мире не было бы химических реакций, не могли бы эволюционировать галактики и звезды. Словом, жизнь там была бы застойно скучна.

Можно было бы ожидать более приятного времяпрепровождения в многомерных мирах. Увы, и это оказывается иллюзией. Исследование уравнения движения

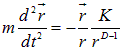
приводит к выводу, что при 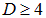в сущности отсутствует финитное движение: оно реализуется только для круговых орбит, да и то является неустойчивым — малейшее возмущение приводит к падению электрона (планеты) на притягивающий центр или его (ее) убеганию на бесконечно большое расстояние. Выходит, в таком мире атомы, планетные системы и все остальное вообще не могло бы образоваться. Никакой стабильности в мирах высшей размерности — вот альтернатива «застойным» маломерным мирам. Только при возможно как устойчивое финитное, так и инфинитное движения. Получается, что трехмерное пространство — единственно удобная форма существования и движения материи, по крайней мере, известных нам ее видов, которые мы изучаем в физике.

Дополнительная информация

http://hea.iki.rssi.ru/~nik/astro/spher.htm — сферическая система координат;

http://edu.ioffe.ru/register/?doc=physica/lect3.ch2.tex — финитное движение, задача Кеплера.

6/7