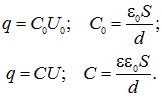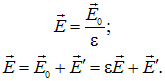3.1. Диэлектрическая проницаемость

Еще М. Фарадей обнаружил, что если между обкладками конденсатора поместить диэлектрическую пластину, то емкость конденсатора возрастает.

На рис. 3.2 показан опыт, в котором демонстрируется зависимость емкости конденсатора от свойств среды между его обкладками. Между пластинами заряженного плоского конденсатора, присоединенного к электрометру, помещают диэлектрик — пластину из оргстекла. При этом показания электрометра уменьшаются, что говорит об увеличении емкости конденсатора. После удаления диэлектрика разность потенциалов увеличивается, возвращаясь к прежнему значению.  

 

Рис. 3.2. Исследование зависимости емкости плоского конденсатора от диэлектрических свойств среды 

Когда изолятор заполняет все пространство между обкладками, емкость конденсатора возрастает в  раз, где безразмерная величина  принимает разные значения для различных материалов. Эта величина называется диэлектрической проницаемостью данного вещества.

Рассмотрим снова плоский конденсатор. Зарядим его и вставим внутрь диэлектрическую пластину (рис. 3.3). 

 

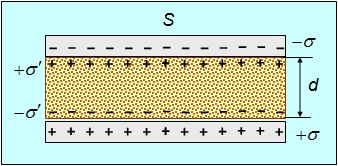
Рис. 3.3. Плоский конденсатор с диэлектрической пластиной между обкладками 

Величины, относящиеся к конденсатору без диэлектрика, будем снабжать индексом 0. Так как заряд конденсатора не меняется при помещении в него диэлектрика, записываем соотношения

(3.1)

Здесь мы использовали экспериментальный факт увеличения емкости конденсатора с диэлектриком в  раз. Из соотношений (3.1) следует, что при том же заряде на обкладках разность их потенциалов U уменьшается в  раз по сравнению с «пустым» конденсатором

Поскольку поле в плоском конденсаторе однородно, получаем следующую связь между напряженностью Е₀ поля в вакууме и в диэлектрике Е

Иными словами, присутствие диэлектрика между пластинами может приводить к уменьшению напряженности электрического поля в конденсаторе. 

Необходимо отметить, что простое уменьшение поля в  раз внутри диэлектрика имеет место тогда и только тогда, когда поверхность диэлектрика представляет собой эквипотенциальную поверхность того поля, которое было бы в отсутствие диэлектрика. Именно этот случай и имеет место при помещении в плоский конденсатор плоскопараллельной диэлектрической пластины, внешние плоские поверхности которой параллельны плоским обкладкам конденсатора и, соответственно, совпадают с двумя эквипотенциальными поверхностями поля конденсатора без диэлектрика. То же самое имеет место, например, в случае помещения в сферический конденсатор сферического слоя диэлектрика с поверхностями концентрическими обкладкам этого конденсатора.

Если, к примеру, в однородное электрическое поле (как в идеальном  плоском конденсаторе) поместить плоскопараллельную диэлектрическую пластину так, что её поверхности составят некоторый угол  с направлением поля и, тем самым, они не будут совпадать с его эквипотенциальными поверхностями, то величина поля внутри этой пластины будет довольно сложным образом зависеть от угла , и будет равна  только при . Не следует также думать, что внесение в поле диэлектрика всегда приводит к уменьшению напряженности поля, она может и возрасти: всё зависит от «геометрии» задачи. Ниже на рисунке 3.4 показано, что при помещении в электрическое поле тонкого длинного диэлектрического стержня параллельно силовым линиям внешнего поля, напряженность поля вне стержня у его концов увеличивается в результате появления на концах стержня «поляризационных» зарядов.

 

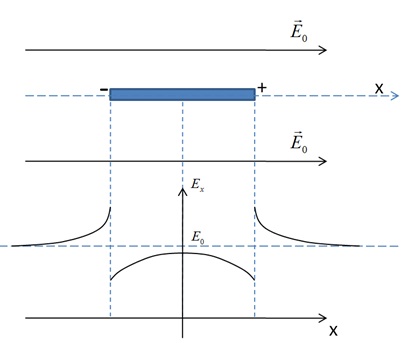
Рис. 3.4. Напряженность поля на оси тонкого диэлектрического стержня 

Уменьшение разности потенциалов между обкладками и увеличение емкости конденсатора мы наблюдали в решенной выше задаче о сферическом конденсаторе с металлической оболочкой между обкладками. Там причина уменьшения разности потенциалов была ясна: на оболочке наводились индуцированные заряды, которые компенсировали внешнее поле от обкладок. Соответственно, электрическое поле существовало только в пространстве, не занятом оболочкой. Если бы оболочка заняла весь объем конденсатора, разность потенциалов между обкладками и поле внутри него стали бы равными нулю. 

В диэлектрике нет зарядов, способных перемещаться по всему его объёму, но идея возникновения на его поверхности каких-то дополнительных зарядов (их называют в этом случае поляризационными или связанными) кажется привлекательной из-за возможности объяснить экспериментальные факты. Поэтому мы принимаем макроскопическую модель, которая, разумеется, должна быть обоснована впоследствии на микроскопическом уровне и проверена на практике вместе со всеми ее следствиями. Мы предположим, что при помещении диэлектрика в электрическое поле на его поверхности возникают поляризационные заряды с плотностью  (рис. 3.5). 

 

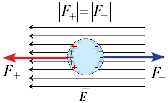
Рис. 3.5. Сферическая частица в однородном электрическом поле напряжённостью Е.
Знаками «+» и «–» показаны связанные заряды, возникшие на поверхности частицы при её поляризации.
Электрические силы, действующие на положительные (F₊) и отрицательные (F_–) связанные заряды, одинаковы 

 Поляризационные заряды создают дополнительное электрическое поле , направленное противоположно полю от зарядов на обкладках (см. рис. 3.3). Это и объясняет меньшую величину результирующего поля Е по сравнению с полем E₀. Действительно, для простейшей геометрии плоского конденсатора (см. выше замечание о форме поверхности диэлектрика) изменение поля в диэлектрике сводится только к изменению величины его напряженности в  раз

(3.2)

Отсюда мы находим, какая часть результирующего поля создается поляризационными зарядами, а какая — зарядами на обкладках

Отрицательный знак указывает на противоположное направление поля поляризационных зарядов. Зная связь поверхностной плотности зарядов с напряженностью создаваемого ими поля

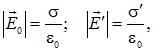
Находим  плотность поляризационных зарядов

 Заметим, что случаю проводника соответствует предел

Действительно, тогда  , а поле внутри материала полностью компенсируется, получаем

откуда

 

Значения e для некоторых диэлектриков приведены в таблице (для газов — при нормальных условиях). 

Таблица

Значения диэлектрической проницаемости для некоторых веществ

 

 

Обратите внимание: одни и те же вещества при разных условиях имеют различные диэлектрические свойства. Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества. 

 

Дополнительная информация 

http://chemister.da.ru/Chemie/Tables/dielectric.htm — диэлектрические проницаемости некоторых веществ;

http://www.radioland.net.ua/contentid-381-page1.html — основные типы диэлектриков, применяемые в конденсаторах;

http://ufn.ru/ufn67/ufn67_11/Russian/r6711n.pdf — статья «Вещества с высокой и сверхвысокой диэлектрической проницаемостью»;

http://www.chipdip.ru/video.aspx?vid=ID000292886&tag=dielectric — видео «Пироэлектрики»;

http://gos-rz.narod.ru/2/20.htm - сегнетоэлектрики, их применение;

http://www.rci.rutgers.edu/~ecerg/projects/ferroelectric.html  — керамические сегнетоэлектрики;

http://www.chipdip.ru/video.aspx?vid=ID000292814&tag=dielectric  — видео «Сегнетокерамика».