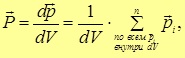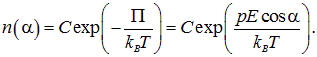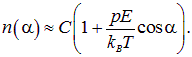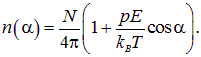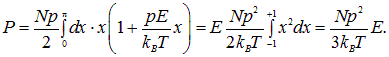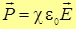3.3. Поляризация диэлектриков

Любое вещество, вне зависимости от его агрегатного состояния и деталей его  атомно-молекулярного устройства, например, атомный, молекулярный или ионный кристалл и т. п., в конечном счете, состоит из положительно заряженных ядер и отрицательно заряженных электронов.

Поэтому механизм поляризации один — это смещение положительных зарядов по поляризующему полю и отрицательных зарядов против поляризующего поля (рис. 3.14). Здесь уместно подчеркнуть, что вещество поляризуется не внешним полем (см., например (3.2) выше), а суммарным полем ,  созданным как сторонними (не принадлежащими диэлектрику) зарядами, так и самим поляризованным веществом. В дальнейшем мы не будет специально это подчеркивать. 

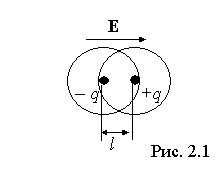
Рис. 3.14. Смещение положительных зарядов по поляризующему полю
и отрицательных зарядов против поляризующего поля 

Видео 3.2. Модель процесса поляризации неполярного диэлектрика.

При исследовании поляризационных свойств конкретных веществ разумно и полезно выделять те главные особенности единого механизма перемещения зарядов под действием поляризующего поля, которые и определяют результат: степень и характер поляризованности вещества. Это приводит к рассмотрению целого ряда «частных» механизмов поляризации, таких как:

• Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля. Самая быстрая поляризация (до  с). Потери энергии отсутствуют.
• Ионная — смещение узлов кристаллической структуры под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки. Время протекания   с, без потерь.
• Дипольная (ориентационная) — связана с ориентацией диполей во внешнем электрическом поле. Протекает с потерями энергии на преодоление сил связи и внутреннего трения.

и многие другие.

Несколько слов по поводу упомянутой выше ионной поляризации, которая имеет место в кристаллах типа поваренной соли NaCl. Под действием поля положительно заряженные ионы натрия Na⁺ и отрицательно заряженные ионы хлора Cl^– смещаются в разные стороны из своих равновесных положений, из-за чего каждая элементарная ячейка кристалла приобретает электрический дипольный момент. Этот пример полезен в следующем смысле: как бы сложно ни был устроен диэлектрик — в данном случае ионный кристалл — его поляризация обусловлена смещением в противоположные стороны положительных и отрицательных зарядов. Вопрос в том, какие конкретно носители заряда способны к такому перемещению: свободные электроны в металле, сильно связанные с ядрами электроны электронной оболочки нейтральных атомов или молекул в газе или жидкости, ионы в узлах кристаллической решетки и так далее. Определяется это тем, как устроен диэлектрик.  

Процессы, происходящие в диэлектрике при его поляризации, можно понять, исходя из представлений о диэлектрике как о среде, состоящей из попарно связанных разноименных зарядов. В отличие от проводников в диэлектриках нет свободных зарядов, которые под действием внешнего поля могут двигаться по всему объему образца. Заряды, входящие в состав молекул диэлектрика, прочно связаны между собой и способны перемещаться только в пределах своей молекулы (или атома), то есть на расстоянии порядка  см. 

Практически во всех тех случаях, когда диэлектрик состоит из электрически нейтральных частиц (атомов и молекул), независимо от его агрегатного состояния, возможно сведение всех «подмеханизмов» поляризации к двум видам. Для этого принято делить все атомы и молекулы и состоящие из них диэлектрики на два класса: 

• Неполярные атомы и молекулы — не имеющие собственного дипольного момента, то есть их собственный дипольный момент в отсутствие поляризующего поля равен нулю: . Это атомы благородных газов  и симметричные молекулы с ковалентной связью типа . Существуют и многоатомные неполярные молекулы. Диэлектрики, состоящие из таких частиц, принято называть неполярными диэлектриками (рис. 3.15);

Рис. 3.15. Поляризация неполярного диэлектрика

• Полярные атомы и молекулы — имеющие отличный от нуля собственный дипольный момент . Это несимметричные молекулы с ковалентной связью типа , а также молекулы с ионной связью типа . Отметим, что у молекул с ионной связью  во много раз больше, чем у молекул с ковалентной связью.  Диэлектрики, состоящие из таких частиц, принято называть полярными диэлектриками (рис. 3.16);

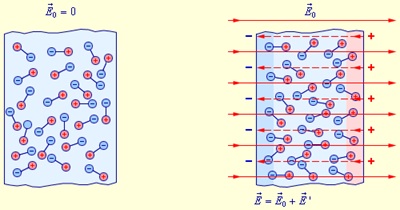
Рис. 3.16. Ориентационный механизм поляризации полярного диэлектрика

Видео 3.3. Модель процесса поляризации полярного диэлектрика.

Здесь — вектор дипольного момента одной молекулы, суммирование ведётся по всем молекулам, находящимся внутри физически бесконечно малого объема   . Например, рассмотрим однородно поляризованный шар (рис. 3.17). 

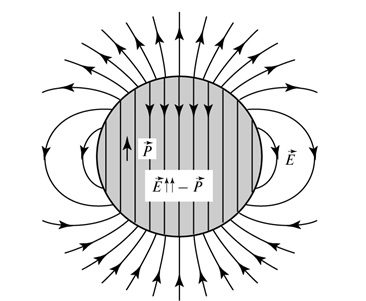
Рис. 3.17. Поляризованность и электрическое поле однородно поляризованного шара 

При поляризации неполярного диэлектрика электронная оболочка атома или молекулы деформируется — электроны смещаются против поляризующего поля, ядра смещаются по полю. Возникает некоторое расстояние между ранее (в отсутствие поляризующего поля) совпадавшими центрами положительных и отрицательных зарядов. В результате атом или молекула приобретают некоторый наведенный дипольный момент. 

Более или менее очевидно, что наведенный дипольный момент будет пропорционален величине внешнего электрического поля. Понять это можно, рассматривая поведение потенциальной энергии П(x) взаимодействия двух частиц, где х — расстояние между ними. Пусть равновесному состоянию соответствует расстояние (частицы находятся в одной точке и дипольный момент отсутствует). При малых отклонениях от положения равновесия в разложении потенциальной энергии в ряд Тейлора можно ограничиться несколькими первыми членами

Учитывая, что первая производная в точке равновесия равна нулю и что вторая производная в этой точке положительна , получаем, что вблизи точки устойчивого равновесия потенциальная энергия ведет себя как

Соответственно, при отклонении от этого положения возникает сила

,

подобная силе упругости при растяжении пружины. Если заряды в молекуле «соединены» такой «пружиной», то при наложении поля Е новое равновесное расстояние между частицами будет определяться соотношением

В результате находим величину возникшего под действием поля дипольного момента

Умножая наведенный дипольный момент на концентрацию поляризованных молекул N/V (N — их полное число в объеме V), получаем поляризованность диэлектрика

Если записать поляризованность (3.16) в виде

где константа (для данного вещества)  по определению есть диэлектрическая восприимчивость вещества, то для , то в рамках данной модели диэлектрическую восприимчивость можно вычислить по нижеследующей формуле

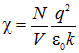
У молекул, называемых полярными, центры положительных и отрицательных зарядов сдвинуты друг относительно друга, поэтому такая молекула имеет собственный дипольный момент. При помещении такой молекулы в электрическое поле её электронная оболочка деформируется, расстояние между центрами зарядов увеличивается и к исходному собственному дипольному моменту добавляется некоторый наведенный дипольный момент. Однако, можно показать, что этот дополнительный наведенный дипольный момент много меньше собственного. Разумеется, это справедливо, если поляризующее поле много меньше поля, существующего внутри молекулы. По порядку величины внутримолекулярное поле равно атомной единице напряженности электрического поля:  В/м. В написанном выражении для атомной единицы напряженности электрического поля  масса электрона,  его заряд,  постоянная Планка. Учитывая, что, например, «пробойная» — приводящая к искровому разряду – напряженность поля для сухого воздуха составляет всего  В/м, то есть на пять порядков меньше, можно утверждать, что в подавляющем большинстве экспериментов наведенным дипольным моментом, при наличии собственного, можно пренебречь. В дальнейшем, при рассмотрении поляризации дипольных диэлектриков, этот эффект (наведение дополнительного момента) учитываться не будет.

Векторы собственных дипольных моментов отдельных молекул в обычном состоянии из-за теплового движения ориентированы хаотически. Поэтому при отсутствии внешнего электрического поля средний суммарный дипольный момент любого физически бесконечно малого объема диэлектрика равен нулю. Другими словами, диэлектрик не поляризован: его поляризованность  равна нулю.

Внешнее электрическое поле стремится ориентировать дипольные моменты молекул параллельно вектору , а тепловое движение этому препятствует, диэлектрик поляризуется, при этом его поляризованность должна зависеть от температуры, а именно: с ростом температуры она должна убывать. Ниже эта зависимость вычисляется, также будет показано, что и в случае полярных диэлектриков их поляризованность пропорциональна напряженности поляризующего поля. Такая поляризация называется ориентационной (рис. 3.18). 

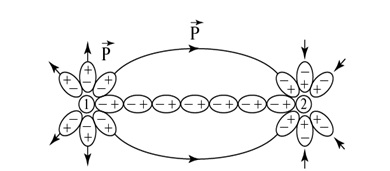
Рис. 3.18. Ориентационная поляризация диэлектрика

В соответствии с формулой (3.8) потенциальная энергия диполя во внешнем поле Е зависит от ориентации диполя

Согласно статистическому закону Больцмана (рис 3.19), описывающему распределение частиц по энергиям во внешнем поле в условиях термодинамического равновесия, число молекул, дипольный момент которых ориентирован под углом , к внешнему полю, определяется как

Здесь С — нормировочная постоянная, значение которой мы найдем позже, Т — абсолютная температура, постоянная Больцмана — k_B = 1,38·10^–23 Дж/К. Вследствие малости дипольного момента молекул, для обычных (не слишком низких) температур показатель экспоненты мал, и мы можем разложить экспоненту в ряд Тейлора, оставляя первые два члена

Подчеркнем, что использование приближенного выражения (3.18) и всех выводов, следующих из него, оправдано при не слишком низких температурах, когда . Не представляет труда точное вычисление с использованием (3.17) вместо приближенного (3.18), которое читатель может проделать самостоятельно.

Интеграл  по полному телесному углу должен дать полное число N  молекул в системе. Поскольку среднее значение косинуса равно нулю, то интегрируется лишь первое слагаемое в (3.18). Так как значение полного телесного угла равно , получаем

Теперь мы знаем постоянную С и можем записать выражение (3.18) в виде

Необходимо определить значение проекции суммарного дипольного момента на направление поля (другие проекции заведомо равны нулю ввиду осевой симметрии задачи). Проекция дипольного момента одной молекулы равна рcosa, следовательно полный дипольный момент Р  всех молекул в единице объема равен

Интеграл по равен , а интеграл по  вычисляется с помощью замены переменной

Находим тогда

Из (3.21) вытекает, что и в случае дипольной ориентационной поляризации вещества поляризованность пропорциональна напряженности электрического поля. Более того, мы нашли зависимость поляризованности  от температуры. Это закон Кюри, который подтверждается на опыте (рис. 3.20).

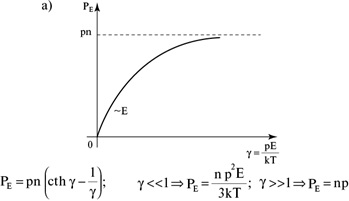
Рис. 3.20. Зависимость поляризованности полярного диэлектрика от температуры (точное решение) 

Подводя итоги данного раздела, мы вкратце повторим основные выводы. Внешнее электрическое поле либо создает дипольные моменты, ориентированные по полю, либо ориентирует дипольные моменты отдельных молекул, и диэлектрик приобретает определенный макроскопический дипольный момент. Вектор  называется поляризованностью  диэлектрика. Он пропорционален напряженности внешнего электрического поля, и эту связь можно представить в виде

где  — коэффициент пропорциональности (его называют диэлектрической восприимчивостью). Коэффициент пропорционален концентрации частиц в диэлектрике и в случае полярного диэлектрика зависит от его температуры. Так как размерность дипольного момента в СИ

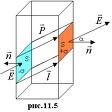
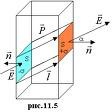
то вектор поляризации в СИ измеряется в Кл/м². Его размерность совпадает с размерностью поверхностной плотности зарядов. Это наводит на мысль, что вектор поляризованности связан с плотностью поляризационных зарядов, возникающих на поверхности и в объеме диэлектрика, помещенного во внешнее поле (рис. 3.21).

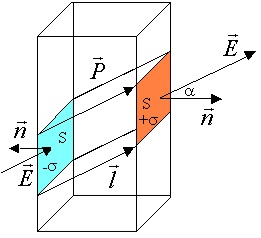
Рис. 3.21. Вектор поляризованности и плотность поляризационных зарядов

Пропорциональность между поляризованностью Р  и напряженностью Е  внешнего электростатического поля объясняется в случае электронной и ионной поляризации тем, что с увеличением Е  растут дипольные моменты отдельных атомов p_i. При дипольной поляризации пропорционально увеличению напряженности внешнего электростатического поля увеличивается степень ориентации векторов p_i. Выше мы нашли общие формулы для диэлектрической восприимчивости при различных видах поляризации. Следует подчеркнуть, что они справедливы для газов: мы не учитывали влияния молекул друг на друга, что допустимо для систем, где частицы не слишком плотно упакованы. Но общий вывод остается справедливым и для конденсированных сред (жидкостей и твердых тел): под действием внешнего электрического поля единица объема диэлектрика приобретает дипольный момент Р; в простейших случаях имеет место линейная зависимость

В полную диэлектрическую восприимчивость диэлектрика дают вклад все три рассмотренных механизма:

Обычно редко бывает, чтобы все доли диэлектрической восприимчивости были одинаково велики. Скажем, в ионных кристаллах дипольная часть вообще отсутствует. Экспериментально вклад каждой доли можно найти, измеряя диэлектрические проницаемости при разных частотах электромагнитной волны. При низких частотах (статическое поле, которым мы сейчас занимаемся) вклад дают все три доли диэлектрической восприимчивости (рис. 3.22).

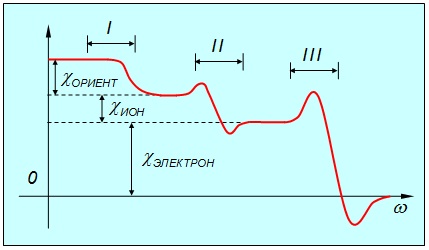
Рис. 3.22. Зависимость полной диэлектрической восприимчивости диэлектрика 
от частоты электромагнитной волны. Указаны диапазоны частот:
I — область радио- и микроволн, II — инфракрасная область, III — ультрафиолетовая область

При повышении частоты первым исчезнет вклад дипольной части: молекулы не будут успевать поворачиваться, следуя быстро изменяющемуся электрическому полю волны. Переход к новому режиму осуществляется обычно при частотах радиодиапазона. При дальнейшем росте частоты исчезнет вклад ионной части: ионы более инерционны, нежели электроны. В диапазоне оптических частот доминирует электронная доля поляризации. При переходе к еще более высоким частотам — за ультрафиолетовой областью — даже электронные облачка не будут успевать следовать за изменениями электрического поля и поляризуемость диэлектрика исчезнет.

Приведем пример: у поваренной соли NaCl диэлектрическая проницаемость в статическом поле равна 5,62, а в поле электромагнитной волны оптического диапазона — всего лишь 2,25. Дипольная поляризуемость в таких кристаллах отсутствует, и различие следует приписать ионной поляризуемости.

Дополнительная информация 

http://science.hq.nasa.gov/kids/imagers/ems/index.html  — электромагнитные волны, шкала электромагнитных волн;

http://science.hq.nasa.gov/kids/imagers/ems/radio.html  — радиоволны;

http://www.nrao.edu/index.php/learn/radioastronomy/radiowaves — радиоволны, источники радиоволн.