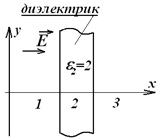
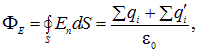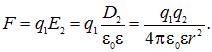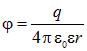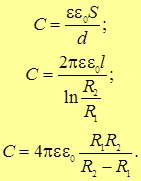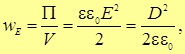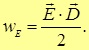3.5. Электростатика диэлектриков

Применим теорему Остроградского — Гаусса к электрическому полю в диэлектрике. Поток вектора напряженности через замкнутую поверхность пропорционален алгебраической сумме зарядов (свободных и поляризационных), находящихся внутри ограниченного этой поверхностью объема

где q_i   — свободные, а q '_i  — поляризационные заряды. Это выражение неудобно, так как в него входят поляризационные заряды, которые, в свою очередь, зависят от напряженности электрического поля в данной точке диэлектрика.

Рассмотрим теперь поток вектора электрического смещения

(3.28)

Так как напряженность поля поляризационных зарядов можно записать в виде

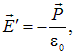
то

(3.29)

Следовательно,

 

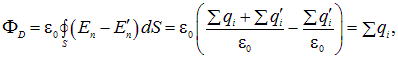
откуда

(3.30)

где q_i   — свободные заряды. Следует подчеркнуть, что линии вектора D  могут начинаться и заканчиваться на свободных зарядах, но не на поляризационных.

Следует обратить внимание на отсутствие в правой части множителя , который имеется в аналогичном выражении для потока вектора напряженности в вакууме. 

Из теоремы Остроградского — Гаусса для точечного заряда q внутри диэлектрика следует

(3.31)

Вектор D  не определяет силу, действующую на заряд со стороны внешнего электрического поля. Силовой характеристикой, по-прежнему, является , то есть . При линейной зависимости от для вычисления силы следует воспользоваться соотношением

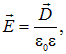
откуда

 

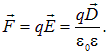
Получим теперь закон Кулона для таких диэлектриков. Свободный заряд q₂ создает в диэлектрике электрическое смещение

откуда следует выражение для силы взаимодействия с другим свободным зарядом q₁

(3.32)

Соответственно, изменится выражение для потенциала, создаваемого свободным зарядом q

(3.33)

и, как следствие, формулы для работы по перемещению свободного заряда в поле и энергии взаимодействия свободных зарядов. Мы замечаем, что по сравнению с аналогичными формулами для систем зарядов в вакууме, для диэлектриков надо произвести замену  Поскольку приведенные выражения являлись основным источником всех прочих соотношений, выведенных нами для вакуума, мы немедленно получаем, например, выражения для емкостей плоского (2.12), цилиндрического (2.14) и сферического (2.17) конденсаторов, заполненных однородным диэлектриком (рис 3.25, 3.26, 3.27, 3.28)

Рис. 3.25. Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик

 

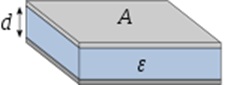
Рис. 3.26. Плоский конденсатор с диэлектриком

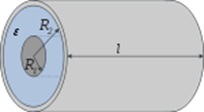
Рис. 3.27. Цилиндрический конденсатор с диэлектриком

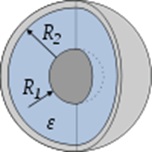
Рис. 3.28. Сферический конденсатор с диэлектриком

Для плотности энергии электрического поля (2.57) теперь можно написать выражение

которое может быть представлено в векторной форме: