6.3. Магнитное поле на оси кругового тока

Напряженность магнитного поля на оси кругового тока (рис. 6.17-1), создаваемого элементом проводника Idl, равна

поскольку в данном случае

Рис. 6.17. Магнитное поле на оси кругового тока (слева) и электрическое поле на оси диполя (справа) 

При интегрировании по витку вектор  будет описывать конус, так что в результате «выживет» только компонента поля вдоль оси 0z. Поэтому достаточно просуммировать величину

(6.10)

Интегрирование

выполняется с учетом того, что подынтегральная функция не зависит от переменной l, а

Соответственно, полная магнитная индукция на оси витка равна

В частности, в центре витка (h = 0) поле равно

На большом расстоянии от витка (h >> R) можно пренебречь единицей под радикалом в знаменателе. В результате получаем

(6.13)

Здесь мы использовали выражение для модуля магнитного момента витка Р_m , равное произведению I на площадь витка  Магнитное поле образует с круговым током правовинтовую систему, так что (6.13) можно записать в векторной форме

Для сравнения рассчитаем поле электрического диполя (рис. 6.17-2). Электрические поля от положительного и отрицательного зарядов равны, соответственно,

так что результирующее поле будет 

(6.15)

На больших расстояниях (h >> l) имеем отсюда

(6.16)

Здесь мы использовали введенное в (3.5) понятие вектора электрического момента диполя . Поле Е параллельно вектору дипольного момента, так что (6.16) можно записать в векторной форме

(6.17)

Аналогия с (6.14) очевидна.

 

Силовые линии магнитного поля кругового витка с током показаны на рис. 6.18. и 6.19 

 

Рис. 6.18. Силовые линии магнитного поля кругового витка с током на небольших расстояниях от провода

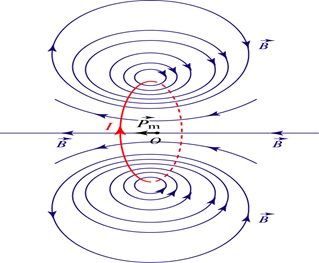
Рис. 6.19. Распределение  силовых линий  магнитного поля кругового витка с током в плоскости его оси симметрии.
Магнитный момент витка направлен по этой оси 

На рис. 6.20 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг кругового витка с током. Толстый медный проводник пропущен через отверстия в прозрачной пластинке, на которую насыпаны железные опилки. После включения постоянного тока силой 25 А и постукивания по пластинке опилки образуют цепочки, повторяющие форму силовых линий магнитного поля.

Магнитные силовые линии для витка, ось которого лежит в плоскости пластинки, сгущаются внутри витка. Вблизи проводов они имеют кольцевую форму, а вдали от витка поле быстро спадает, так что опилки практически не ориентируются. 

 

Рис. 6.20. Визуализация силовых линий магнитного поля вокруг кругового витка с током 

Пример 1. Электрон в атоме водорода движется вокруг протона по окружности радиусом а_B = 53 пм (эту величину называют радиусом Бора по имени одного из создателей квантовой механики, который первым вычислил радиус орбиты теоретически) (рис. 6.21). Найти силу эквивалентного кругового тока и магнитную индукцию В поля в центре окружности.

Рис. 6.21. Электрон в атоме водорода 

Решение. Заряды электрона и протона одинаковы по величине (е) и противоположны по знаку. На электрон действует сила кулоновского притяжения протона, создающая центростремительное ускорение

откуда находим угловую скорость движения электрона по круговой орбите

Период обращения электрона вокруг ядра равен

Если представить себе воображаемую площадку, ортогональную траектории электрона, то за время Т через нее проходит заряд е. Поэтому сила эквивалентного тока равна

Скорость движения электрона равна v = а_B = 2,18·10⁶ м/с. Движущийся заряд создает в центре орбиты магнитное поле

 

Этот же результат можно получить с помощью выражения (6.12) для поля в центре витка с током, силу которого мы нашли выше

Пример 2. Бесконечно длинный тонкий проводник с током 50 А имеет кольцеобразную петлю радиусом 10 см (рис. 6.22). Найти магнитную индукцию в центре петли.

Рис. 6.22. Магнитное поле длинного проводника с круговой петлей 

Решение. Магнитное поле в центре петли создается  бесконечно длинным прямолинейным проводом и  кольцевым витком. Поле от прямолинейного провода направлено ортогонально плоскости рисунка «на нас», его величина равна (см. (6.9))

Поле, создаваемое кольцеобразной частью проводника, имеет то же направление и равно (см. 6.12)

Суммарное поле в центре витка будет равно

 

 

Дополнительная информация 

http://n-t.ru/nl/fz/bohr.htm — Нильс Бор (1885–1962); 

http://www.gumer.info/bibliotek_Buks/Science/broil/06.php  — теория Бора атома водорода в книге Луи де Бройля «Революция в физике»;

http://nobelprize.org/nobel_prizes/physics/laureates/1922/bohr-bio.html — Нобелевские премии. Нобелевская премия по физике 1922 г. Нильс Бор.