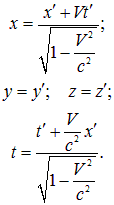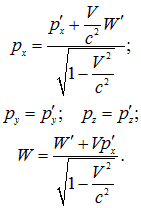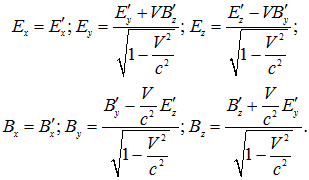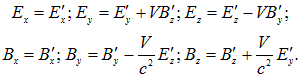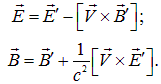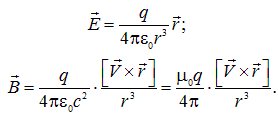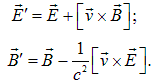6.7. Преобразования Лоренца для электромагнитного поля
Связь между электричеством и магнетизмом не исчерпывается похожестью ряда соотношений. В сущности, оба эти поля суть разные проявления единого электромагнитного поля. В курсе механики мы говорили о принципе относительности, о том, что все законы природы должны быть инвариантными при переходе из одной инерциальной системы отсчета в другую. Однако электрическое и магнитное поля сами по себе, по отдельности, явно не удовлетворяют этому принципу. Действительно, находясь в инерциальной системе отсчета К, возьмем заряд q, движущийся прямолинейно и равномерно со скоростью v. Он создает кулоновское электрическое поле и, помимо этого, магнитное поле, вектор индукции которого дается выражением (6.2). Свяжем с зарядом систему отсчета К ', которая также будет инерциальной. В этой системе отсчета заряд покоится, и создаваемое им поле будет чисто электростатическим. Выходит, электрическое и магнитное поля не имеют абсолютного характера. При переходе к другой системе отсчета они должны преобразовываться друг через друга (рис. 6.33).
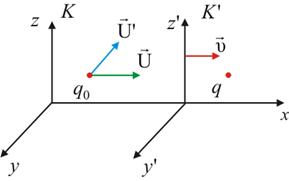
Рис. 6.33. Заряд покоится в движущейся системе отсчета
Вспомним преобразования Лоренца для пространственных координат и времени
|
|
(6.36) |
Не забудем, что аналогичные преобразования связывают импульс и энергию частицы в разных системах отсчета
|
|
(6.37) |
Станем ли мы теперь удивляться, что электрическое и магнитное поля в разных системах отсчета также связаны преобразованиями Лоренца
|
|
(6.38) |
Напомним, что величины со штрихом относятся к системе отсчета К ', которая движется относительно системы К вдоль оси х со скоростью V.
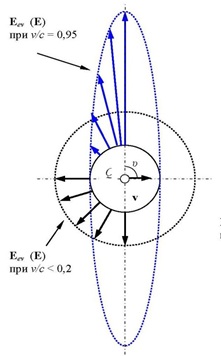
Из преобразований Лоренца следует, что электрическое поле движущегося заряда вытягивается в направлении перпендикулярном скорости (рис. 6.34).
Рис. 6.34. Электрическое поле движущегося заряда
Заметим, что формулы преобразований Лоренца для электромагнитного поля отличаются от преобразований для пространства-времени или энергии-импульса тем, что не преобразуются компоненты полей вдоль линии движения системы отсчета К ' (то есть вдоль оси 0х). Чтобы проиллюстрировать это, рассмотрим лабораторную систему отсчета К, в которой имеется электрическое поле Е, но нет магнитного (В = 0). В каком случае наблюдатель движущейся системы отсчета К ' тоже будет наблюдать лишь чисто электрическое поле Е ' без примеси магнитного (В ' = 0)? Ответ следует из формул (6.38) при подстановке туда нулевых значений для В, В ': из второго уравнения сразу вытекает Е 'y = Е 'z = 0, а из первого — Еу = Ez = 0. Иными словами, такое возможно, когда электрическое поле (не обязательно однородное) направлено вдоль движения системы отсчета К '.
Уравнения электромагнетизма изначально были инвариантны относительно этих преобразований, так что теория относительности вполне безболезненно совместилась с электромагнитной теорией, в то время как классическая механика подверглась существенной ревизии. Вместо обоснования справедливости преобразований (6.38), что выходит за рамки нашего курса, мы познакомимся еще с одним их следствием.
Поскольку мы пока занимаемся в основном нерелятивистской физикой, упростим преобразования Лоренца для случая, когда скорость системы отсчета К ' много меньше скорости света: V << с. В этом случае, как уже отмечалось, квадратные корни
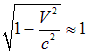
и преобразования (6.38) принимают вид
|
|
(6.39) |
Эти уравнения можно записать в векторной форме
|
|
(6.40) |
Вернемся к нашей заряженной частице, покоящейся в системе К '. В этой системе магнитное поле отсутствует (В ' = 0), а электрическое поле дается законом Кулона
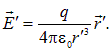
Поскольку предполагается V << с, мы используем преобразования Галилея для пространственных координат и временных интервалов, так что радиус-вектор, проведенный от частицы в точку наблюдения, одинаков в обеих системах отсчета: r = r '. Подставляя указанные выражения для В ', Е ' в преобразования (6.40), получаем
|
|
(6.41) |
Здесь мы использовали соотношение (6.3)
![]()
Первое уравнение (6.41) — обычное кулоновское поле заряда q, второе — магнитное поле движущегося заряда (6.2). Таким образом, даже классический магнетизм — это проявление релятивистских эффектов. Электрическое и магнитное поля оказываются неразрывно связанными друг с другом в единое электромагнитное поле, конкретное проявление которого зависит от системы отсчета.
Пример. Самолет летит горизонтально со скоростью 250 м/с в магнитном поле Земли с магнитной индукцией 50 мкТл, направленной вертикально вниз. Какое электромагнитное поле будут наблюдать пассажиры самолета?
Решение. Направим ось 0х системы лабораторной отсчета К, связанной с Землей, вдоль маршрута самолета, так что его скорость запишется в виде
![]()
Ось 0z направим вертикально вверх, так что магнитная индукция описывается вектором
![]()
Нам надо найти электрическое и магнитное поля в движущейся системе отсчета К ', связанной с самолетом. Поскольку скорость самолета много меньше скорости света, мы можем применить формулы (6.40). Для удобства, однако, мы используем обратные формулы, получаемые заменой штрихованных величин на нештрихованные и изменением знака скорости: V = –v:
|
|
(6.42) |
Так как в лабораторной системе электрического поля нет (Е = 0), то из второго уравнения сразу следует, что В ' = В: магнитное поле для авиапассажиров останется тем же, что и для проводивших их в полет родственников. Однако, в самолете появится еще и электрическое поле. Его напряженность, как вытекает из первого уравнения, равна
|
|
(6.43) |
Мы использовали здесь тот факт, что векторное произведение двух ортов дает третий орт
![]()
60 м на их концах создается разность потенциалов ![]() — величина небольшая, но доступная измерениям.
— величина небольшая, но доступная измерениям.
Дополнительная информация
http://www.galileogalilei.ru/ — Галилео Галилей (1564–1642). Биография. Сочинения. Размышления. Философия. Преобразования Галилея;
http://n-t.ru/nl/fz/lorentz.htm — Хендрик Лоренц (1853–1928).